Discussion :

[aziz1015]

Bonjour,

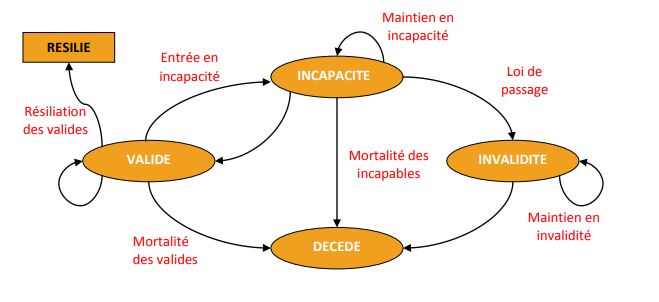
j'ai une question sur les probabilités dans un modèle à états comme sur l'image jointe.

Si je veux par exemple avoir la probabilité d'être incapable avec ce modèle à partir de tous les états possibles. Est ce bien :

( proba d'être valide *1/2*proba de passer de valide à incapable + proba d'être invalide *(1- taux de passage d'incapable à invalide) + proba de maintien en incapacité )*(1-1/2*proba de décès)*(1 - proba de résiliation)

Par avance, je vous remercie pour votre aide.



Abdel-aziz

[tbc92]

Les facteurs 1/2 , pourquoi ?
Et par ailleurs, : proba d'être invalide *(1- taux de passage d'incapable à invalide) : c'est un peu incohérent. Je pense que tu voulais écrire proba d'être incapable*(1- taux de passage d'incapable à invalide)

Je ne te donne pas la réponse, en particulier parce que ce n'est pas totalement clair, je ne suis pas du tout certain de savoir répondre à la question. Mais les 2 points ci dessus, c'est sûr, ça ne va pas.

En fait, tu as écrit une longue formule, mais tu n'expliques pas chaque étape de ton calcul.
Pour moi, une formule sans explication, c'est quasi certain, c'est faux.
Si tu écris une formule, et si tu es capable d'expliquer cette formule, alors c'est bon signe, c'est probablement bon.

[aziz1015]

Les facteurs 1/2 , pourquoi ?
Et par ailleurs, : proba d'être invalide *(1- taux de passage d'incapable à invalide) : c'est un peu incohérent. Je pense que tu voulais écrire proba d'être incapable*(1- taux de passage d'incapable à invalide)

Je ne te donne pas la réponse, en particulier parce que ce n'est pas totalement clair, je ne suis pas du tout certain de savoir répondre à la question. Mais les 2 points ci dessus, c'est sûr, ça ne va pas.

En fait, tu as écrit une longue formule, mais tu n'expliques pas chaque étape de ton calcul.
Pour moi, une formule sans explication, c'est quasi certain, c'est faux.
Si tu écris une formule, et si tu es capable d'expliquer cette formule, alors c'est bon signe, c'est probablement bon.

Bonjour,

Merci pour votre réponse. Je m'explique :

Pour moi, la probabilité d'être incapable dans ce schéma peut se résumer en 3 évènements :

la probabilité d'être valide et de devenir incapable par la suite


que je traduis par : proba d'être valide *1/2*taux de passage de valide à incapable

1/2 parce que je suppose qu'un valide a autant de chance de chances de mourir que de devenir incapable

OU

la probabilité d'être invalide et de devenir incapable

proba d'être invalide *taux de passage d'invalide à incapable

OU

La probabilité d'être incapable et de se maintenir dans cet état
proba d'entrée en incapacité*proba de maintien en incapacité
ET
de ne pas avoir fait de résiliation
ET
de ne pas être décédé (1- proba de résiliation)*(1-1/2*proba de décès)

J'ai essayé de vous expliquer mon raisonnement en tenant compte de vos remarques. Pourriez-vous me dire ce qui ne va pas svp ?

Merci

[Guesset]

Bonjour,

Le texte n'est pas en conformité avec le schéma qui :

• ne prévoit pas de transition d'invalidité vers incapacité.
• ne prévoit de sortie du contrat que pour les valides, mais le décès devrait entrainer une résiliation me semble-t-il.
• ne prévoit pas d'entrée sous contrat (certainement pour les seuls valides) ce qui mécaniquement mènera le nombre de valides à 0.

La probabilité devrait être temporelle (par mois, an ou autre). A défaut, la probabilité intemporelle du décès est 1. Si c'est une probabilité instantanée, il n'y a aucune combinaison de probabilités car une combinaison suppose plusieurs transitions d'états en séquence ce qui ne saurait être instantané.

Par exemple, sauf erreur de ma part, la probabilité d'être valide et de devenir incapable est, en instantané, seulement p(valide -> incapable).
Si les probabilités sont, par exemple, mensuelles, la probabilité devient p(valide -> incapable)/(1 - p(incapable-> valide)*p(valide -> incapable))*p(maintien incapacité) si on tient compte d'allers-retours valide <-> incapable dans la période. L'idée est que pour qu'un valide soit dans l'état d'incapacité à la fin du mois, il faut qu'il passe dans cet état peut être avec des allers-retours et qu'il y reste.

En considérant qu'il n'y a, par individu, qu'une transition possible par période (par exemple journalière), on simplifie singulièrement les calculs (quasi idem probabilité instantanée).

Je conseillerais de numéroter les états pour pouvoir écrire p(1,2) pour la probabilité de passer de l'état 1 à l'état 2 ce qui serait plus lisible? Si valide est l'état 1 et incapacité l'état 2, l'expression précédente devient plus lisible : p(1,2)/(1 - p(2,1)*p(1.2))*p(2,2).

Il est préférable de ne mettre les valeurs numériques qu'à la fin des calculs.

Salutations

[aziz1015]

Bonjour,

Merci pour votre retour.

Bonjour,

Le texte n'est pas en conformité avec le schéma qui :

• ne prévoit pas d'entrée sous contrat (certainement pour les seuls valides) ce qui mécaniquement mènera le nombre de valides à 0.

Je ne comprends pas trop cette phrase.

La probabilité devrait être temporelle (par mois, an ou autre). A défaut, la probabilité intemporelle du décès est 1. Si c'est une probabilité instantanée, il n'y a aucune combinaison de probabilités car une combinaison suppose plusieurs transitions d'états en séquence ce qui ne saurait être instantané.

La probabilité est par année

En considérant qu'il n'y a, par individu, qu'une transition possible par période (par exemple journalière), on simplifie singulièrement les calculs (quasi idem probabilité instantanée).

Je ne peux pas considérer cela dans mon modèle. Pour résumer, j'ai déjà comme inputs par âge et par pas de temps d'un an : les taux d'entrée en incapacité, les qx du décès, les taux de résiliation, les taux de retour à l'état sain. Quand je passe d'une année à l'autre, je dois faire intervenir la probabilité d'être en vie (1-proba de décès).

Par exemple, sauf erreur de ma part, la probabilité d'être valide et de devenir incapable est, en instantané, seulement p(valide -> incapable).

Pourquoi il n'y pas de 1/2 ? Quand un individu est à l'état valide, il peut soit passer à l'état incapable, soit passer à l'état décédé non ?

J'essaie de comprendre votre formule. Partons de votre proposition :

• 1 représente l'état valide
• 2 représente l'état incapable
• 3 représente l'état décédé
• 4 représente l'état invalide

D'où :

• à t=0, proba d'être valide est de 100%
• à t=1, p(1,1) = 100%*(1-p(1,3))*(1-p(1,2))*(1-proba de résiliation)
  

Est ce correct ? Je continue :

Être incapable se traduit pour moi par : 1->2 ou 2->1->2 ou 2->2

Donc Toujours à t=1, la probabilité d'être incapable est pour moi :

p(2) = 100%*(1-p(1,3))*(1-p(1,2))*(1-proba de résiliation)*( p(1,2)+ p(2,2)*p(2,1)*p(1,2)+p(2,2) )

Je conseillerais de numéroter les états pour pouvoir écrire p(1,2) pour la probabilité de passer de l'état 1 à l'état 2 ce qui serait plus lisible? Si valide est l'état 1 et incapacité l'état 2, l'expression précédente devient plus lisible : p(1,2)/(1 - p(2,1)*p(1.2))*p(2,2).

Tout ça pour dire que je ne comprends pas la division dans votre formule.

merci encore pour votre aide.

[tbc92]

Quand un individu est valide il peut :
- soit rester valide
- soit entrer en incapacité
- soit décéder.
Et il peut aussi résilier son contrat


Donc le 1/2 n'est pas justifié, ce serait plutôt 1/3 ou éventuellement 1/4.
Mais ce n'est pas 1/3 ni 1/4 non plus.
En fait, partant de l'état 'Valide', il y a 4 flèches.
Il faudrait mettre des poids (des proportions, des taux ...) à côté de chaque flèche.
Et du coup :

Quand un individu est valide il peut :
- soit rester valide avec une probabilité P11
- soit entrer en incapacité avec une probabilité P12
- soit décéder. avec une probabilité P13
Normalement, P11+P12+P13 =1

Et il peut aussi résilier son contrat avec une probabilité P15


C'est un exercice 'scolaire', ou c'est autre chose ?