Discussion :

[zenux]

Bonjour,

Je n'arrive pas à comprendre pourquoi les deux code sources suivants m'affichent un résultat différent:

Fonctionne:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

gl_Position =  mProjection * mView * mModel * vec4(vertexPosition, 1.0)

Ne fonctionne pas:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
vec4 positiont = mProjection * mView * mModel * vec4(vertexPosition, 1.0);
positiont /= positiont.w;
gl_Position = positiont;

J'ai toujours pensé que "W" était utilisé pour permettre une translatation quand on multiplie un vecteur avec une matrice. Une fois la multiplication fini, on pouvais diviser les composantes du vecteur par W, non ?

Merci d'avance.

[LastSpear]

Bonjour

J'ai toujours pensé que "W" était utilisé pour permettre une translatation quand on multiplie un vecteur avec une matrice. Une fois la multiplication fini, on pouvais diviser les composantes du vecteur par W, non ?

On divise par w en générale que pour la position des vertices, pour avoir une projection non orthogonal (ou dite en perspective) de tes objets sur ta surface de rendu, si tu veux mettre un angle de projection d'une camera par exemple. (je ne dis pas qu'on ne l'utilise pas pour d'autre calcul) Mais tu peu très bien programmer une projection orthogonal sur ta surface de rendu si nécessaire, auquel cas tu ne dois pas diviser par gl_Position.w.

projection non orthogonal (perspective):


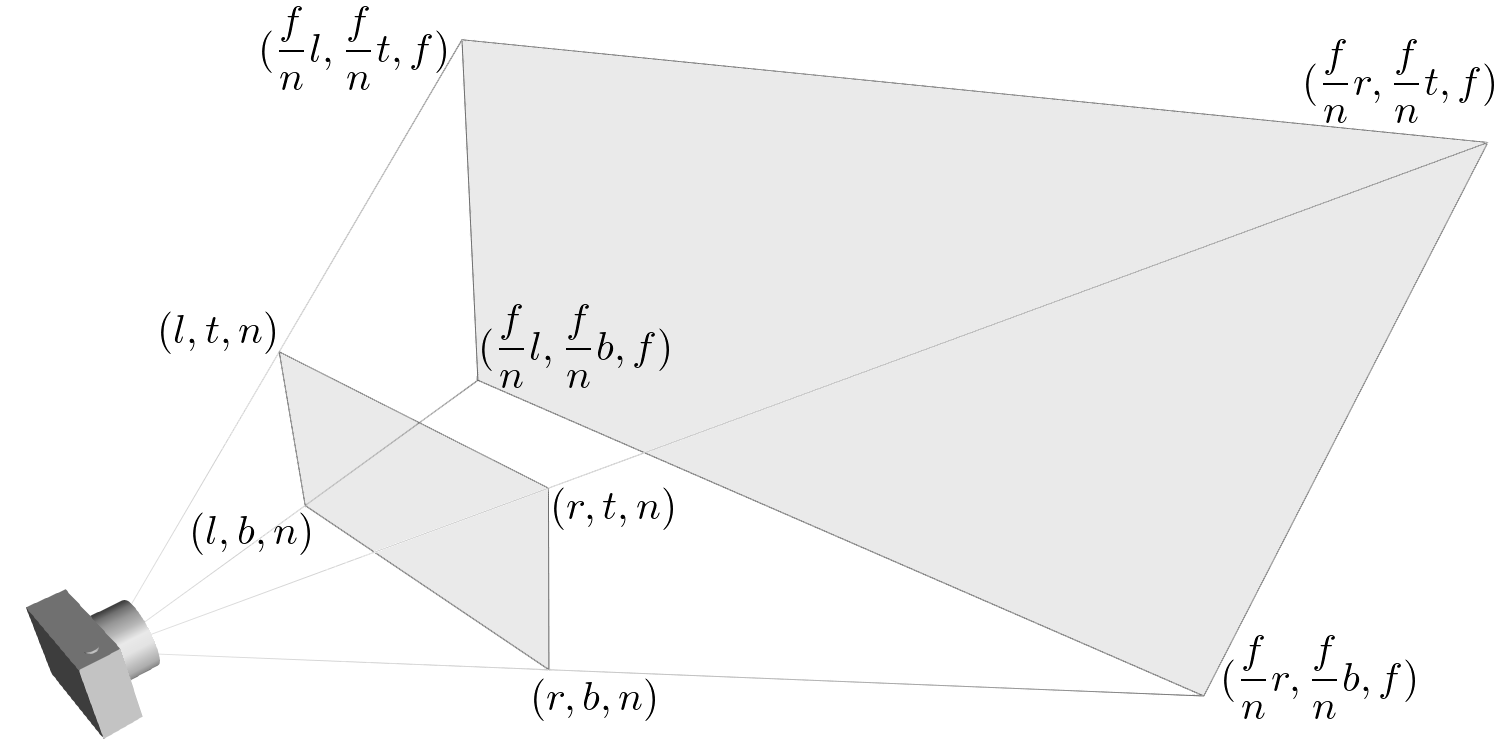
projection orthogonal :



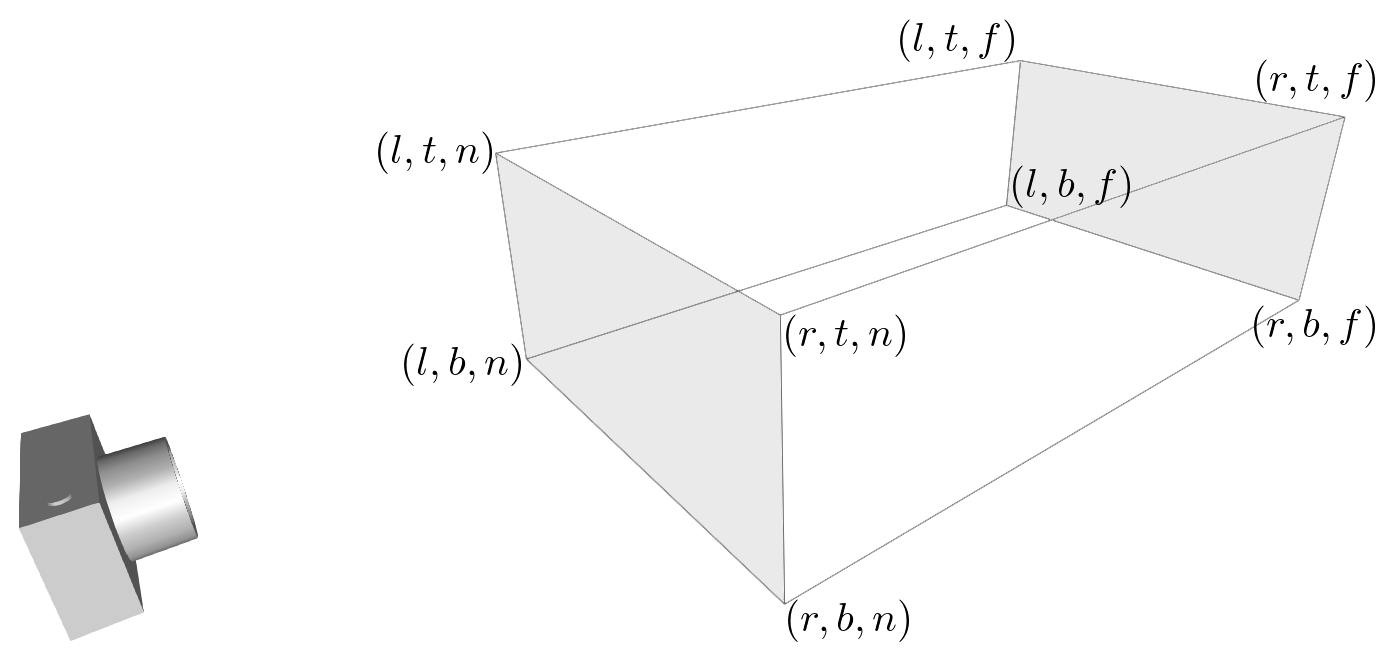
Donc la nécessité de diviser par gl_Position.w depend si tu es en GL_MODELVIEW ou en GL_PROJECTION, si tu est en GL_MODELVIEW, opengl fera automatiquement la division de gl_Position par sa composante w.

donc en GL_MODELVIEW, le shader qui convient est celui ci :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

gl_Position =  mProjection * mView * mModel * vec4(vertexPosition, 1.0);

sinon, c'est c'est l'autre

Personnellement, pour un rendu en perspective (donc en projection non orthogonal), je me met en en GL_MODELVIEW, et je laisse OpenGL se débrouiller comme il sais bien le faire avec la division par w ainsi que ses corrections de perspective. Tu n'as pas besoin de le codé toi même dans ton vertex (ainsi que dans le geometry ou tessellation évaluation) shader. Mais si tu insiste pour le faire quand même, passe en GL_PROJECTION, et donc OpenGL affichera tout bêtement ton triangles au coordonné gl_Position.xy de ton viewport, et gl_Position.z dans le depth buffet.

D'un point de vu générale, lors d'une multiplication matricielle interprété comme un changement de repère, w = 1.0 pour effectivement avoir la translation en compte. Mais tu peut aussi avoir w = 0.0 pour réorienté les normals, car la translation n'est plus prise en compte.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

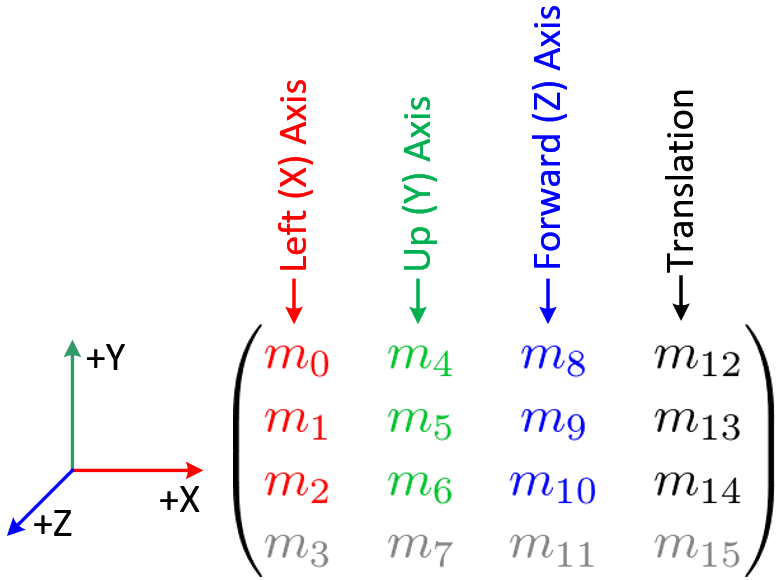
NormalOut = normalize((mModel * vec4(NormalIn, 0.0)).xyz) ;

Il est donc pas nécessaire de chargé une deuxième matrice liée au repère de ton objet pour les normals.

Note que si NormalIn est déjà normé, et que mModel est une matrice orthonormé, alors NormalOut sera aussi normé, donc normalize n'est plus nécessaire, ainsi tu gagnes en performance.

Libre a toi d'avoir d'autre interprétations du produit matricielle bien sur (barycentres pour la tessellation etc ...) :cool:

J'espère avoir été suffisamment clairs.

[zenux]

Merci pour cette superbe réponse mais j'ai toujours du mal à comprendre

1) Je travail avec OpenGL 3.3 et donc il n'y a plus de GL_MODELVIEW / GL_PROJECTION à ma connaissance !
Je pensais qu'un OpenGL <3.3, le mode GL_PROJECTION permetait de charger une matrice de projection (orthogonal ou non) une fois pour toute (en général) et le mode GL_MODELVIEW permet de charger une matrice model et view qui doit être updaté à chaque fois qu'un object ou la caméra bouge.

2)

GL_MODELVIEW, opengl fera automatiquement la division de gl_Position par sa composante w

Si je fait ma division par W et ensuite OpenGL fait la sienne : quel est le problème ? Le division d'OpenGL par W=1.0 n'aura aucun effet.

3)

OpenGL se débrouiller comme il sais bien le faire avec la division par w ainsi que ses corrections de perspective

Corrections de perspective ? Mon vertex est déjà multiplié par la matrice de projection mProjection: qu'est-ce que OpenGL doit faire de plus ?

[LastSpear]

A oui avec OpenGL 3.3, çà change. Il n'y a, en effet, plus ce contrôle de GL_MODELVIEW et GL_PROJECTION. Alors une partie ma réponse précédente servira (peut être) aux les lecteurs qui programment sur des versions antérieur. Je me disais bien que c'était très hold school par rapport à ta question.

Quelque soit ton utilisation, les coordonnées de gl_Position.xyz seront automatiquement divisé par gl_Position.w
C'est très clairement dit paragraphe 2.13 Coordinate Transformations =>Documentation OpenGL 3.3

Si je fait ma division par W et ensuite OpenGL fait la sienne : quel est le problème ? Le division d'OpenGL par W=1.0 n'aura aucun effet.

Bien sur. Et j'ai même entendu parlé que si le compilateur avait explicitement un gl_Position.w = 1.0 ; alors il désactivai la division par w automatiquement par optimisation du calcul. Mais je me porte pas garant.

Corrections de perspective ? Mon vertex est déjà multiplié par la matrice de projection mProjection: qu'est-ce que OpenGL doit faire de plus ?

Et bien il faut "culé" le vertex avant de faire la division par w. En effet, si la composante z et w sont négative, alors ta division par w va te ressortir un z positif donc sera affiché, alors que ton vertex est sensé être "derrière" ton plan de projection donc derrière la camera, donc pas affiché.

Or tu ne peut pas faire un genre de "discard" toi même dans le vertex shader pour çà. Donc si tu dev toi même la division par w, tu dois t'assuré qu'aucun vertex ne soit derrière ton plan de projection. Sinon c'est tout simplement une erreur de conception.

Donc si tu veux quelque chose de fiable, contente toi de spécifié à OpenGL w, et il va faire le boulo à ta place.

[zenux]

Merci pour vos réponses et désolé pour ma réponse tardive.

Et bien il faut "culé" le vertex avant de faire la division par w. En effet, si la composante z et w sont négative, alors ta division par w va te ressortir un z positif donc sera affiché, alors que ton vertex est sensé être "derrière" ton plan de projection donc derrière la camera, donc pas affiché.

A ma connaissance, une matrice de projection va modifier tous les points visibles de la scène entre les coordonnées -1 et 1 (division par W comprise).
Pour la coordonnée Z: -1 = near plane & 1 = far plane.

J'ai bon essayé de multiplier n'importe quel point non visible dans la scène par ma matrice de projection et de diviser par W, je n'arrive jamais à obtenir une coordonée Z entre -1 et 1. Je me trompe ?
Donc il me semble que le rôle d'OpenGL est de simplement diviser les gl_Position par W et d'éliminer ceux qui ne se trouvent pas entre -1 et 1, non ? Ou est-ce que je me trompe ?

Merci d'avance.

[LittleWhite]

OpenGL enlève les coordonnées avant -1 et après 1, car elles sont simplement, hors écran

[DonQuiche]

J'ai toujours pensé que "W" était utilisé pour permettre une translatation quand on multiplie un vecteur avec une matrice. Une fois la multiplication fini, on pouvais diviser les composantes du vecteur par W, non ?

Je me permets de clarifier l'explication. Si tu veux faire une successions de rotation ou de translations, ton vecteur aura toujours un "w" égal à 1 car tes matrices auront toujours pour troisième ligne : "0 0 0 1". Il suffit de regarder par exemple cette composée d'une translation et d'une rotation:
x' = cos(a).x + sin(a).y + x0
y' = -sin(a).x + cos(a).y + y0
z' = z + z0
w = w
Tout ceci s'écrit très bien avec des matrices puisque celles-ci représentent des transformations du type "x' = ax + by + cz + d".

Maintenant, si l'on veut écrire une matrice de perspective, ça se complique. Les équations pour une perspective simple sont les suivantes: x' = x / z et y' = y / z. Là, nous sommes coincés, les matrices ne permettent pas de faire ce genre de transformations. Donc, on utilise une astuce. On écrit à la place:
x' = x
y' = y
z' = z
w' = z
Et OpenGL se charge de diviser ensuite par "w". On parle pour les coordonnées non-divisées de "coordonnées homogènes". C'est ce que tu dois fournir à gl_position.



Moralité de l'histoire : avec une matrice de projection orthogonale, w vaudrait toujours "1" et les deux codes produiraient le même résultat. Avec une perspective, en revanche, "w" sera différent de 1 et il est normal que les deux codes produisent un résultat différent.


PS : translation pas translatation.