Discussion :

[Mani8]

Bonjour,

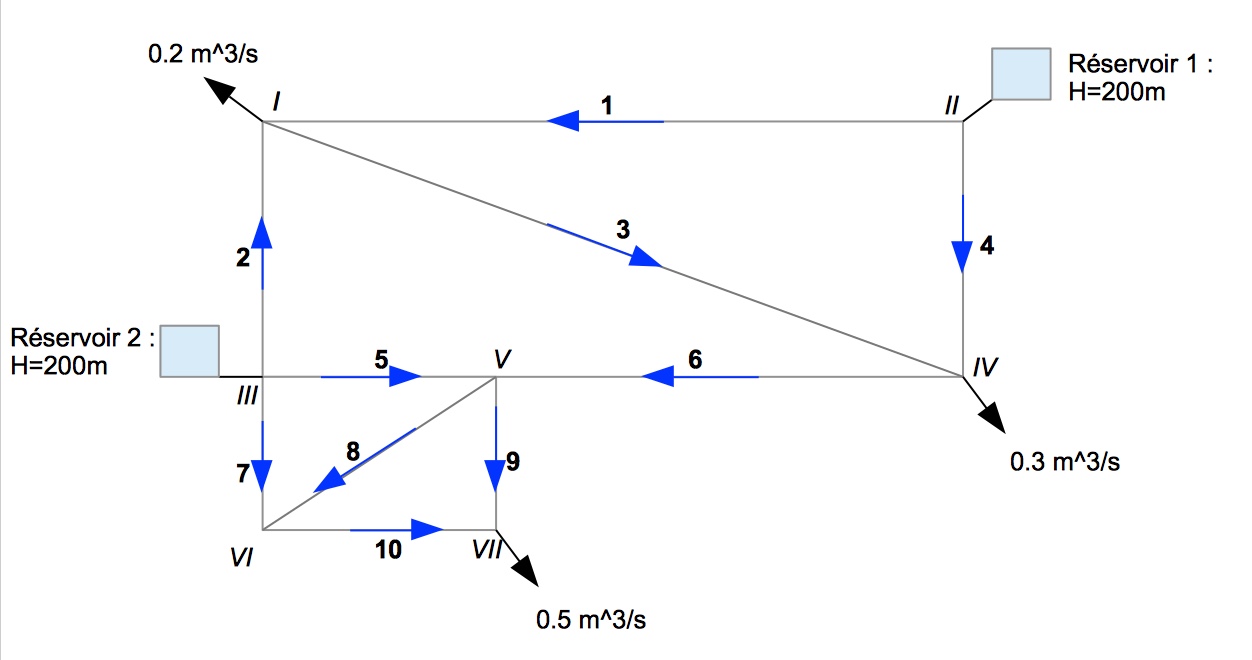
Je cherche à implémenter dans Matlab un algorithme permettant de "résoudre" un réseau de tuyauterie (c'est à dire déterminer le débit Q et la direction du flux dans chaque tuyau ainsi que la hauteur piézométrique H à chaque intersection).
Le résultat obtenu est bien celui que j'attends mais pour une raison que je ne parviens pas à identifier la vitesse de convergence de l'algorithme est très lente (en témoignent les graphes de la déviation relative maximale et du résidu maximal).

Quelqu'un aurait-il un conseil pour accélérer la convergence ? Mon problème vient-il d'une fonction que j'aurais mal utilisé ?

Le code:

Code matlab :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
clear
clear all
close all
 
% Fluid and gravity
rho = 1e3;
mu  = 1e-3;
g   = 9.81;
 
% Colebrook formula
colebrook = @(Re,rr,la) 1/sqrt(la)+2*log10(rr/3.71+2.51/Re/sqrt(la));
 
% Deposit
h1 = 200;
h2 = 200;
 
% Pipe data
L1 = 600;
L2 = 400;
L3 = 900;
L4 = 400;
L6 = 350;
L7 = 600;
L9 = 300;
L10 = 500;
L11 = 300;
L12 = 350;
 
D1 = 0.5;
D2 = 0.5;
D3 = 0.5;
D4 = 0.5;
D6 = 0.5;
D7 = 0.5;
D9 = 0.3;
D10 = 0.3;
D11 = 0.3;
D12 = 0.3;
 
v_L  = [L1 L2 L3 L4 L6 L7 L9 L10 L11 L12];
v_D  = [D1 D2 D3 D4 D6 D7 D9 D10 D11 D12];
 
v_r = 1e-3*ones(1,size(v_L,2));
v_rr = v_r./v_D;
 
% Initial lambda values. Starting with Reynolds infinity.
v_la = 0.25./(log10(v_rr/3.71)).^2;
 
% Initial conditions
v_Q = 0.1*ones(1,size(v_L,2));
v_H = [10 h1 h2 10 10 10 10];
 
%Connectivity matrix
    % 1  2  3  4  6  7  8 
E = [-1  1  0  0  0  0  0; %1
     -1  0  1  0  0  0  0; %2
      1  0  0 -1  0  0  0; %3
      0  1  0 -1  0  0  0; %4
      0  0  1  0 -1  0  0; %6
      0  0  0  1 -1  0  0; %7
      0  0  1  0  0 -1  0; %9
      0  0  0  0  1 -1  0; %10
      0  0  0  0  1  0 -1; %11
      0  0  0  0  0  1 -1];%12
 
 %Declare known C values 
 x=0;
 v_C=[-0.2 x x -0.3 0 0 -0.5];
 y = [0 1 1 0 0 0 0]; %logic matrix: 0 when C is known, 1 when H is known
 
 %%....Main Loop....%%
 
 %Iteration limits
 maxiter = 1000;
 tol = 1e-3;
 inc = 1;
 res = 1;
 iter = 0;
 
 %Creation of solution storage matrices
 Q_results = zeros(size(v_Q,2),maxiter);
 H_results = zeros(size(v_H,2),maxiter);
 inc_results = zeros(1,maxiter);
 res_results = zeros(1,maxiter);
 v_sol = [v_Q v_H(1,1) v_H(1,4:size(v_H,2))];
 
 %...........MAIN LOOP.............%
 while (inc>tol) && (res>tol) && (iter<maxiter)
 
 iter = iter+1;
 
 %Storage of previous iteration results
 Q_results(:,iter)=v_Q';
 H_results(:,iter)=v_H';
 v_sol_old = v_sol;
 
 %Calculate Reynolds numbers from Q
 v_vel = 4*v_Q/pi./v_D.^2;
 v_Re  = abs(rho*v_vel.*v_D/mu);
 
 %Get the new lambdas
 for i = 1:size(v_Q,2)
    v_la(i) = fzero(@(x)colebrook(v_Re(i),v_rr(i),x),v_la(i));
 end
 
 %Obtain matrix M
 v_F = 8/pi^2/g./v_D.^4.*v_la.*v_L./v_D;
 v_K = v_F.*abs(v_Q);
 K = diag(v_K);
 M = E'/K*E;
 
 %Obtain A and b
 A=M*diag(1-y)-diag(y);
 b=-M*(v_H.*y)'+(v_C.*(1-y))';
 
 %Solve the system
 X=A\b;
 
 %Extract the new H and C values 
 v_H=X';
 v_H(2)=h1;
 v_H(3)=h2;
 v_C(2)=X(2);
 v_C(3)=X(3);
 
 %Re-evaluate Q
 v_Q=(K\E*v_H')';
 
 %Update solution matrix
 v_sol = [v_Q v_H(1,1) v_H(1,4:size(v_H,2))];
 
 %Relative increment of solution
 inc = norm((v_sol-v_sol_old)./v_sol,inf);
 %inc = norm((v_Q-v_sol_old(1:10))./v_Q,inf);
 inc_results(iter) = inc;
 
 %Residual of system
 res = norm(v_sol-v_sol_old,inf);
 %res = norm(v_Q-v_sol_old(1:10),inf);
 res_results(iter) = res;
 
 end
 
 %Plots
 inc_results(iter+1:maxiter) = [];
 res_results(iter+1:maxiter) = [];
 
 figure(1)
 subplot(211)
 semilogy(1:iter,inc_results)
 box on,grid on
 xlabel('iteration')
 ylabel('relative increment')
 
 subplot(212)
 semilogy(1:iter,res_results)
 box on,grid on
 xlabel('iteration')
 ylabel('residue')

Le système à résoudre:


Détail de l'algorithme:
1- Première estimation des valeurs Q et H + estimation arbitraire de l'orientation des flux (correspond aux flèches bleues sur le schéma). Ces orientations sont consignées dans une matrice de connectivité c.a.d une matrice ayant autant de colonnes qu'il y a d'embranchements et autant de lignes qu'il y a de tuyaux. Les éléments de cette matrice valent 1 là d'où le flux part pour un tuyau donné, -1 là où il arrive et 0 partout ailleurs. Cette matrice s’appellera E.

2- Calcul de la vitesse d'écoulement v dans chaque tuyau à partir de Q=(pi*D^2/4)*v

3- Calcul du nombre de Reynolds pour chaque tuyau

4- Utilisation de la formule de Colebrook pour déterminer le coefficient de Darcy (pour la première utilisation de la formule, j'utilise une valeur du coefficient de Darcy correspondant à un nombre de Reynolds tendant vers l'infini c.a.d.
lambda=0.25/( log(eps/3.71)^2 ) )


5- Pour chaque tuyau, je calcule la valeur K=lambda/(2*g*A^2) * L/D * abs(Q) puis je crée une matrice diagonale (les K(i) formant donc une diagonale avec les autres éléments de la matrice égaux à 0)

6- On peut alors obtenir une nouvelle matrice M=E' * inv(K) * E qui présente l'avantage de vérifier l'équation suivante:
M*H=C où C désigne la somme des débits à chaque embranchement

7- Il faut alors distinguer les croisements où on connait H (II et III) et ceux où on connaît C (tous les autres).
On va construire deux nouvelles matrices. Pour chaque embranchement i :
A: - Quand C est connu, la colonne i de A est égale à la colonne i de M
- Quand H est connu, l'élément A(i,i) vaut -1 et le reste de la colonne vaut 0
b:Il s'agit un vecteur. Chaque b(i) prend initialement la valeur -1*Somme(M(i,j)*H(j)) (somme des M(i,j)*H pour tous les H connus)
- Quand C est connu, b(i)=b(i)+C
- Quand H est connu, passer à l'élément suivant
NB: J'utilise un vecteur logique (y) pour obtenir chacune de ces deux matrices avec 1 seule ligne de code

8- On peut alors résoudre A*x=b où x est un vecteur contenant pour chaque embranchement:
C si H était connu
H si C était connu

9- Je ré-obtiens alors le vecteur Q via l'équation Q=inv(K)*E*H

10- Je calcule la déviation relative par rapport à l'itération précédente ainsi que le résidu et compare à une tolérance, l'algorithme boucle alors jusqu'à ce que l'une de ces valeurs soit reconnue comme satisfaisante