Résolution de la conjecture Collatz et problème de Syracuse

**toumic2.0** · 28/05/2023, 11h43

Nom : conjectCollatzPublicCode_Profondeur1.png
Affichages : 202
Taille : 340,0 Ko

**toumic2.0** · 05/06/2023, 12h03

Envoyé par tyrtamos

Bonjour

Problème intéressant! Mais il vaudrait mieux parler de "vérification" plutôt que de "résolution" puisque cette conjecture n'a jamais été résolue.

Une page web pour la définition:
https://fr.wikipedia.org/wiki/Conjecture_de_Syracuse

Voilà un petit code pour cette vérification:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
def syracuse(n):
    """ Calcule la conjecture de Syracuse pour n
    """
    suite, k = [n], n
    while k != 1:
        k = k//2 if k%2==0 else k*3+1
        suite.append(k)
    return suite

La vérification consiste à constater que la suite se termine toujours par "1", quelque soit n

Si on reprend l'exemple de wikipedia: n=15

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
n = 15
suite = syracuse(n)
print(n, suite)
15, [15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]

Curieusement, il y a un vocabulaire particulier à cette conjecture:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
print("temps de vol:", len(suite)-1)
 
for i, x in enumerate(suite):
    if x<n:
        break
print("temps de vol en altitude:", i-1)
 
print("altitude maximale:", max(suite))

Ce qui affiche

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
temps de vol: 17
temps de vol en altitude: 10
altitude maximale: 160

Autre exemple cité par wikipedia:
n = 27. Résultat:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
27 [27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
temps de vol: 111
temps de vol en altitude: 95
altitude maximale: 9232

Il faudrait faire ce calcul pour des millions de valeurs n pour vérifier que la suite se termine toujours avec une valeur "1", et jusqu'à présent, personne n'a trouvé le contraire. Mais cette conjecture n'aura pas été pour autant résolue mathématiquement.

Et ça va bien ? ☺

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Nombre à évaluer : 64origine : 64 . Appartient à la section :  64
Dico =  [64, 32, 16, 8, 4, 2]                Longueur Terminale =  6
Dico =  [62]                  Longueur =  1
Dico =  [60, 30]                  Longueur =  2
Dico =  [58]                  Longueur =  1
Dico =  [56, 28, 14]                  Longueur =  3
Dico =  [54]                  Longueur =  1
Dico =  [52, 26]                  Longueur =  2
Dico =  [50]                  Longueur =  1
Dico =  [48, 24, 12, 6]                  Longueur =  4
Dico =  [46]                  Longueur =  1
Dico =  [44, 22]                  Longueur =  2
Dico =  [42]                  Longueur =  1
Dico =  [40, 20, 10]                  Longueur =  3
Dico =  [38]                  Longueur =  1
Dico =  [36, 18]                  Longueur =  2
Dico =  [34]                  Longueur =  1
 
 
 Résultats globaux
Longueur terminale =  6  Longueur exposant de 2
Nombre    listes =  16  Nombre total des listes
Partie    listes =  5  Nombre de parties trilog. Il reste =  0
Section   listes =  4  Longueur de la sous-liste [1, 2, 3, 4, 6]
 
 
 Résultats partiels
Ci:  1 [62, 58, 54, 50, 46, 42, 38, 34] Quantités (cumul, partiel) (8, 8) 
*    Nbr liste//c=  8
Ci:  2 [60, 52, 44, 36] Quantités (cumul, partiel) (16, 8) 
*    Nbr liste//c=  4
Ci:  3 [56, 40] Quantités (cumul, partiel) (22, 6) 
*    Nbr liste//c=  2
Ci:  4 [48] Quantités (cumul, partiel) (26, 4) 
*    Nbr liste//c=  1
Ci:  6 [64] Quantités (cumul, partiel) (32, 6) 
*    Nbr liste//c=  1

**tyrtamos** · 05/06/2023, 15h24

Bonjour

J'ai toujours beaucoup de mal à vous comprendre, mais au moins, vous ne reculez pas devant le boulot!

Avez-vous une question concernant mon code?

**toumic2.0** · 06/06/2023, 02h22

Envoyé par tyrtamos

Bonjour

J'ai toujours beaucoup de mal à vous comprendre, mais au moins, vous ne reculez pas devant le boulot!

Avez-vous une question concernant mon code?

Non votre message nous éclaire sur ce sujet de réflexion, il est simple et amusant à cause de son côté "aéroporté".

Mais c'est sans compter sur mon côté "astronaute", qui par cet enfin réalise un excellent voyage numérique avec ce menu du chef.

Vous avez bien compris que ce développement des nombres pairs et nécessaire à la création de d'informations concernant le parcours de Syracuse☺
Comme une première fois, les résultats ont été obtenus par rapport à des listes créées (ce qui prend trop de temps lors de très nombreux chiffres),
le deuxième essai se fera avec des équations mathématiques permettant ainsi de régler le temps à sa plus basse mesure...
@ bientôt

**toumic2.0** · 09/06/2023, 02h51

Quand on dit que les nombres pairs consécutifs alternent un dédoublement sur deux, on est loin d'avoir tout dit.

Pour donner suite au programme précédent, j'ai enfin réalisé le code qui permet de connaitre le nombre de fois qu'un nombre pair peut être divisé par deux tout en restant de type pair.

C'est une première mouture, excusez la beauté des variables ☺

Le code produit un dictionnaire, avec les quantités de dédoublements incluses, je vous laisse tester (pour celà il faut activer les prints)

Cette information peut trouver une utilité lors des opérations de Syracuse*

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
 
# Démultiplication(/2) ☺
# Version 5 Produit un dictionnaire."""
 
 
def action(choix):
    originel = choix  # Attention :choix: change de valeur
    secteur, primitives = 0, []
    while choix > 1:  # Délimiter la section terminale du choix
        choix /= 2
        secteur += 1
        primitives.append(choix)
    section = 2**secteur
    ('originel :', originel, '. Appartient à la section : ', 2**secteur)
    ('primitives[-1] =', primitives[-1], '(Avant zéro) | Secteurs =', secteur, '\n')
    '# Résultats Globaux : Sections. Listes.'
    section_max = 2**secteur  # Valeur max de la section
    section_min = (section_max//2)+2  # Valeur min de la section
    nombres_all = section_max//4  # Nombre de listes dans la section
    (' section_max =', section_max, '. section_min =', section_min)
    "# Longueur de la plus grande sous_liste, à l'axe (min/max-1)"
    axe = axe_unity = (((nombres_all-1)//2)*2) + section_min  # Calcul de l'axe terminal
    long = axe_unity_long = secteur - 2  # Valeur de la première grande liste
    # Algorithme introspectif
    'Ordre des axes : 0=Terminal. 1=Axe haut. 2=Axe bas.'
    axes_plus, y = {}, 0  # Liste des axes par paires successives,
    while long:
        spaxes_22 = ((axe - (section_min-2)) // 2)
        spaxes_units22 = (spaxes_22)+ (section_min-2)  # Nouvel axe bas
        spaxes_2333 = (axe - spaxes_units22) + axe  # Nouvel axe haut
        if not axe in axes_plus.keys() and not axe%2 and axe >= section_min:
            axes_plus[axe] = long  # Axe terminal
        if long == axe_unity_long - y:
            axe = spaxes_units22
        long -= 1  # Longueur de liste en baisse
        if not spaxes_2333 in axes_plus.keys() and not axe%2 and axe >= section_min:
            axes_plus[spaxes_2333] = long
        if not spaxes_units22 in axes_plus.keys() and not axe%2 and axe >= section_min:
            intervalle = spaxes_2333 - spaxes_units22
            axes_plus[spaxes_units22] = long, intervalle
        y += 1
    inter, tag = list(axes_plus.keys()), False
    for key in inter:
        if len(str(axes_plus[key])) > 1:
            bas = key
            ('key:', key, 'bas:', bas)
            while 1:
                bas += axes_plus[key][1]
                if bas > section_max:
                    break
                elif bas == originel:
                    print("originel pair", bas, 'Long =', axes_plus[key][0])
                    tag = True
                    break
        if tag:
            break
    (' axes_plus =', axes_plus)
 
 
if __name__ == "__main__":
    # Version et interface de saisie
    ('Version-5')
    while 1:
        choix = int(input("Nombre pair à évaluer : "))
        if not choix%2:
            action(choix)
            break

**wiztricks** · 09/06/2023, 13h06

Envoyé par toumic2.0

Pour donner suite au programme précédent, j'ai enfin réalisé le code qui permet de connaitre le nombre de fois qu'un nombre pair peut être divisé par deux tout en restant de type pair.

Soit votre code ne fait pas ce que vous dites soit il fait tellement d'autres choses qu'on a des difficultés à y retrouver cela.
note: croyez vous que votre long monologue ait quelque intérêt?

- W

**toumic2.0** · 10/06/2023, 09h45

Envoyé par wiztricks

Soit votre code ne fait pas ce que vous dites soit il fait tellement d'autres choses qu'on a des difficultés à y retrouver cela.
note: croyez vous que votre long monologue ait quelque intérêt?

- W

Intéressant pour le problème de Syracuse, oui !
Car à chacun des nombres impairs l'opération (n*3+1) crée une ascendance (contrairement aux nombres pairs).
Si vous trouvez que le schèma des nombres pairs est inutile, c'est votre choix.
Si je vous dérange signalez mon incapacité à rester membre aux responsables du site.

Voici ce que répond le code avec le nombre :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
 
Nombre pair à évaluer : 56
originel pair 56 Long = 3

Ce qui correspond au message :
05/06/2023, 12h03

toumic2.0

Nombre à évaluer : 64origine : 64 . Appartient à la section : 64
Dico = [64, 32, 16, 8, 4, 2] Longueur Terminale = 6
Dico = [62] Longueur = 1
Dico = [60, 30] Longueur = 2
Dico = [58] Longueur = 1
Dico = [56, 28, 14] Longueur = 3
Dico = [54] Longueur = 1
Dico = [52, 26] Longueur = 2
Dico = [50] Longueur = 1
Dico = [48, 24, 12, 6] Longueur = 4
Dico = [46] Longueur = 1
Dico = [44, 22] Longueur = 2
Dico = [42] Longueur = 1
Dico = [40, 20, 10] Longueur = 3
Dico = [38] Longueur = 1
Dico = [36, 18] Longueur = 2
Dico = [34] Longueur = 1

Il est important de s'intéresser aux descendances des nombres pairs, losqu'ils sont divisés par 2, et combien de fois il peut être divisé par 2.

**tyrtamos** · 10/06/2023, 17h34

Bonjour

Le nombre de fois qu'un nombre pair quelconque peut être divisé par 2 est facile à calculer. Il s'agit en fait d'une partie d'un algorithme de décomposition en facteurs premiers par la méthode des divisions:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
##############################################################################
def nb2(n):
    """Calcule le nombre de fois qu'on peut diviser n par 2
    """
    c = 0 # compteur
    while True:
        if n%2==0:
            c += 1
            n //= 2
        else:
            break
    return c

Par ailleurs, on peut remarquer qu'à chaque fois qu'on applique la règle destinée aux nombre impairs (x*3+1), on obtient un nombre pair.

Si on calcule à partir de nombres impairs croissants la valeur obtenue paire, et qu'on cherche le nombre de fois que cette valeur peut être divisée par 2, on trouve quelque chose intéressant:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
for i in range(1, 100, 2):
    j = i*3+1
    print(i, j, nb2(j))

Ce qui donne pour tous les nombres impairs de 1 à 99:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

La valeur de la dernière colonne a l'air d'être aléatoire, mais elle ne l'est pas: il y a un cycle. Par exemple, les 2 se retrouvent tous les 4 nombres impairs. Idem pour tous les autres, avec une périodicité différente.

En poursuivant, peut-être pourrait-on trouver une formule qui permette de calculer la taille de la série sans en calculer les termes? Et, pourquoi pas, prouver ainsi mathématiquement la conjecture? Mais il y a eu tant de mathématiciens compétents qui n'ont pas réussi que je ne m'y attaquerai pas. C'était tout de même amusant à faire...

**toumic2.0** · 11/06/2023, 12h26

Envoyé par tyrtamos

Bonjour

Le nombre de fois qu'un nombre pair quelconque peut être divisé par 2 est facile à calculer. Il s'agit en fait d'une partie d'un algorithme de décomposition en facteurs premiers par la méthode des divisions:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
##############################################################################
def nb2(n):
    """Calcule le nombre de fois qu'on peut diviser n par 2
    """
    c = 0 # compteur
    while True:
        if n%2==0:
            c += 1
            n //= 2
        else:
            break
    return c

Par ailleurs, on peut remarquer qu'à chaque fois qu'on applique la règle destinée aux nombre impairs (x*3+1), on obtient un nombre pair.

Si on calcule à partir de nombres impairs croissants la valeur obtenue paire, et qu'on cherche le nombre de fois que cette valeur peut être divisée par 2, on trouve quelque chose intéressant:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
for i in range(1, 100, 2):
    j = i*3+1
    print(i, j, nb2(j))

Ce qui donne pour tous les nombres impairs de 1 à 99:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

La valeur de la dernière colonne a l'air d'être aléatoire, mais elle ne l'est pas: il y a un cycle. Par exemple, les 2 se retrouvent tous les 4 nombres impairs. Idem pour tous les autres, avec une périodicité différente.

En poursuivant, peut-être pourrait-on trouver une formule qui permette de calculer la taille de la série sans en calculer les termes? Et, pourquoi pas, prouver ainsi mathématiquement la conjecture? Mais il y a eu tant de mathématiciens compétents qui n'ont pas réussi que je ne m'y attaquerai pas. C'était tout de même amusant à faire...

À visualiser dans une fenêtre à part !

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
 
# tyrtamos
 
 
##############################################################################
def nb2(n):
    """Calcule le nombre de fois qu'on peut diviser n par 2
    """
    c = 0 # compteur
    while True:
        if n%2==0:
            c += 1
            n //= 2
        else:
            break
    return c
 
 
for i in range(1, 100, 2):  # Séquence des nombres impairs
    j = i*3+1
    print(i, j, nb2(j))
 
 
 
 
# Précisions parfois utiles à la compréhension du problème
# Pourquoi a-t'on besoin de créer un code compliqué ?
"""Les choses ne sont pas si simples que ça, uniquement parce que la complexité n'apparaît pas."""
# Par exemple le code Python "n//2" : Donne en retour un cumul(c) où "if not n%2" !
"""À ce niveau actuel, où il y a le cumul(c), qui ne donne aucune autre information."""
# Quand on à la chance de connaitre un peu les nombres pairs, on connait leur hiérarchisation ..
 
 
# En utilisant le problème de Syracuse appliqué sur le nombre 62, on ne se doute pas qu'on peut traverser
# plusieurs niveaux hiérarchiques parmis les nombres pairs. Exemple, celui-ci : {16: 4, 12: 2, 14: 1, 10: (1, 4)}.
"""
251 Nombre*3+1 = 106.0  _________________________Après traitement fonction.traite(n*3+1)
.*=  66     originel 106.0 section 1 .         66 key_inter
98 FINAL
99 axes_plus.keys()  dict_keys([128, 96, 112, 80, 88, 72, 76, 68, 70, 66])
 {128: 7, 96: 5, 112: 4, 80: (4, 32), 88: 3, 72: (3, 16), 76: 2, 68: (2, 8), 70: 1, 66: (1, 4)}
100 axes_global.keys()  dict_keys([128, 256, 512, 1024, 2048, 4096, 8192, 16384])
101 
103 En attente du prochain appel de fonction.traite()           Fin de fonction.action()"""
# Ci-dessus = key_inter(66 += [axes_plus[66][1]]), jusqu'à ce que 66 devienne 106.
"""
251 Nombre*3+1 = 160.0  _________________________Après traitement fonction.traite(n*3+1)
.*=  160     originel 160.0 section 5 .         66 key_origine
98 FINAL
99 axes_plus.keys()  dict_keys([256, 192, 224, 160, 176, 144, 152, 136, 140, 132, 134, 130]) 
 {256: 8, 192: 6, 224: 5, 160: (5, 64), 176: 4, 144: (4, 32), 152: 3, 136: (3, 16), 140: 2, 132: (2, 8), 134: 1, 130: (1, 4)}
100 axes_global.keys()  dict_keys([128, 256, 512, 1024, 2048, 4096, 8192, 16384])
101 
103 En attente du prochain appel de fonction.traite()           Fin de fonction.action() """
# Ci-dessus = key_origine(160 in [axes_plus.keys()])
"""
251 Nombre*3+1 = 16.0  _________________________Après traitement fonction.traite(n*3+1)
.*=  16     originel 16.0 section 4 .         64 key_majeure
98 FINAL
99 axes_plus.keys()  dict_keys([16, 12, 14, 10]) 
 {16: 4, 12: 2, 14: 1, 10: (1, 4)}
100 axes_global.keys()  dict_keys([128, 256, 512, 1024, 2048, 4096, 8192, 16384, 16])
101 
103 En attente du prochain appel de fonction.traite()           Fin de fonction.action() 
"""
# Ci-dessus = key_majeure(16 = [max(axes_plus.keys())])
'À bon entendeur ☺

**Sve@r** · 28/06/2023, 20h25

Bonjour

Envoyé par toumic2.0

Car à chacun des nombres impairs l'opération (n*3+1) crée une ascendance (contrairement aux nombres pairs).

Déjà, tout nombre impair quel qu'il soit, peut s'écrire sous forme "2k+1", "k" étant un entier.
De là 3n+1 donne 3(2k+1) + 1 soit 6k + 4 soit 2(3k+2) qui est donc un nombre pair. Donc tout nombre impair qui passe par cette suite donne obligatoirement un nombre pair. Qui sera ensuite, conformément à la règle, divisé par 2 au tour suivant.
Dé là, on peut créer une collatz raccourcie qui, pour tout nombre impair "n", donne alors (3n + 1)/2 (et on gagne un tour de boucle sans nuire au but qui est de voir jusqu'où on va).

Envoyé par toumic2.0

Il est important de s'intéresser aux descendances des nombres pairs, losqu'ils sont divisés par 2, et combien de fois il peut être divisé par 2

Je ne pense pas. Car soit il est une puissance parfaite de 2 et il finira par donner au final 2^0 (soit 1, nombre final de la conjecture), soit il ne l'est pas et il finira par donner un impair (et le nombre d'opérations ayant amené ce résultat importe peu). Donc savoir combien de fois il peut être divisé par 2 n'aide en rien à conclure sur la conjecture (qui est "quel que soit le nombre de départ on finit à 1"). Remarque si on modifie cette conjecture en "quel que soit le nombre de départ on finit à une puissance parfaite de 2" cela ne change rien au nombre final.

Envoyé par toumic2.0

Mon approche est bien détaillée et en aucun cas ne peut être contredite.

En aucun cas évidemment. Tu es tellement brillant...

Envoyé par toumic2.0

Les nombres pairs consécutifs quand ils sont divisés par deux entrainent dans tous les cas un coup sur deux un nombre impair, (l'autre c'est qu'il est un nombre pair.

Vous ne pouvez donc pas me contredire sans aucun exemple, ainsi vos réponses sont explicitement inappropriées et complètement négativistes, c'est votre droit.

Aucun exemple. Juste moi je pars de 1024 et j'obtens 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2 et 1 ; soit un impair et 10 pairs. C'est ça le "un coup sur deux" ???

Envoyé par toumic2.0

En poursuivant, peut-être pourrait-on trouver une formule qui permette de calculer la taille de la série sans en calculer les termes?

Non. Tant qu'on n'arrivera pas à modéliser mathématiquement l'expression "s'il est pair/s'il est impair" on ne pourra jamais réduire cette suite en fonction.

Envoyé par tyrtamos

Le nombre de fois qu'un nombre pair quelconque peut être divisé par 2 est facile à calculer. Il s'agit en fait d'une partie d'un algorithme de décomposition en facteurs premiers par la méthode des divisions:

Oui... c'est juste log(n)/log(2)...

**wiztricks** · 29/06/2023, 11h17

Envoyé par Sve@r

Déjà, tout nombre impair quel qu'il soit, peut s'écrire sous forme "2k+1", "k" étant un entier.
De là 3n+1 donne 3(2k+1) + 1 soit 6k + 4 soit 2(3k+2) qui est donc un nombre pair.

Suivant la parité de k, le résultat sera une fois sur deux divisible une seule fois par 2. (la répétition de 1 x 1 x 1 x... dans les sorties de Tyrtamos). Un peu de calcul montrerait que les x sont multiples de 4 et plus (une fois sur 2).
Et je suis d'accord avec Sve@r, on a juste changé de problème (montrer qu'on arrive à une puissance de 2 plutôt qu'à 1) sans avoir plus de solution.

- W

**tyrtamos** · 29/06/2023, 13h28

Bonjour Sve@r

Envoyé par Sve@r

Citation Envoyé par toumic2.0
En poursuivant, peut-être pourrait-on trouver une formule qui permette de calculer la taille de la série sans en calculer les termes?

Non. Tant qu'on n'arrivera pas à modéliser mathématiquement l'expression "s'il est pair/s'il est impair" on ne pourra jamais réduire cette suite en fonction.

C'est moi qui ait dit ça, et non toumic2. Comme je l'ai montré, la constatation de "cycles" dans la suite suggère une capacité de prévision. Comme je l'ai dit, je n'irai pas plus loin, mais ce serait dommage de fermer la porte à toute idée de recherche. Si personne n'a réussi la démonstration, personne n'a prouvé qu'elle était impossible...

**Sve@r** · 29/06/2023, 13h43

Envoyé par tyrtamos

personne n'a prouvé qu'elle était impossible...

Probablement parce qu'elle est vraie (et qu'effectivement tout nombre finit fatalement par retomber soit sur un nombre déjà testé soit sur une puissance de 2).
Mais je crois que ce qui rend cette démonstration impossible c'est que cette suite n'en n'est pas une au sens mathématique. Une suite mathématique c'est une suite où tout terme Un+1 peut être calculé à partir des opérateurs mathématiques classiques (addition, soustraction, etc) appliqués sur le terme précédent Un.
Dans une suite (une vraie) on peut dire "Un+1=Un/2" ou "Un+1=3*Un + 1" et de là, on peut assez souvent arriver à établir Un+1 en fonction de n (c'est d'ailleurs un problème assez souvent posé aux collégiens).
Or l'évaluation "si c'est pair/si c'est impair" n'est pas une opération mathématique. On ne peut pas écrire "truc(2)=1" ou "truc(3)=10".

A la limite je pourrais poser la conjecture de Svear qui dirait

si le nombre est pair on le divise par 2
si le nombre est impair on le multiplie par 7
si le nombre est premier on le multiplie par 3 et on lui enlève 4

Et ensuite on pourrait regarder où on va avec ça. Ca pourrait être sympa mais ça ne serait pas non plus une suite.

**tyrtamos** · 29/06/2023, 14h52

Envoyé par Sve@r

Mais je crois que ce qui rend cette démonstration impossible c'est que cette suite n'en n'est pas une au sens mathématique. Une suite mathématique c'est une suite où tout terme Un+1 peut être calculé à partir des opérateurs mathématiques classiques (addition, soustraction, etc) appliqués sur le terme précédent Un.

Les ouvrages mathématiques qui parlent de la conjecture de Syracuse n'ont pas cette limite (ex: https://fr.wikipedia.org/wiki/Conjecture_de_Syracuse). On a bien une suite de nombres (ici entiers naturels), et on a bien une relation de récurrence permettant de calculer le nombre suivant, à partir du précédent. Cette relation est plus un "algorithme" de récurrence plutôt qu'une formule, mais ce n'est pas interdit. Cependant, il est vrai que quand c'est une formule de récurrence, c'est plus pratique, et on sait tout ce qu'on peut tirer comme avantages des suites arithmétiques et géométriques pour ne prendre que celles-là.

Bref, ce n'est pas encore cette fois que je deviendrai célèbre avec cette démonstration. Dommage...

**toumic2.0** · 29/06/2023, 16h27

Envoyé par Sve@r

Bonjour

Une remontée impaire systématique pour une descente "aléatoire" au grès des cascades des nombres pairs,
est-ce que cette descente aléatoire a-t'elle un algorithme régulier ?

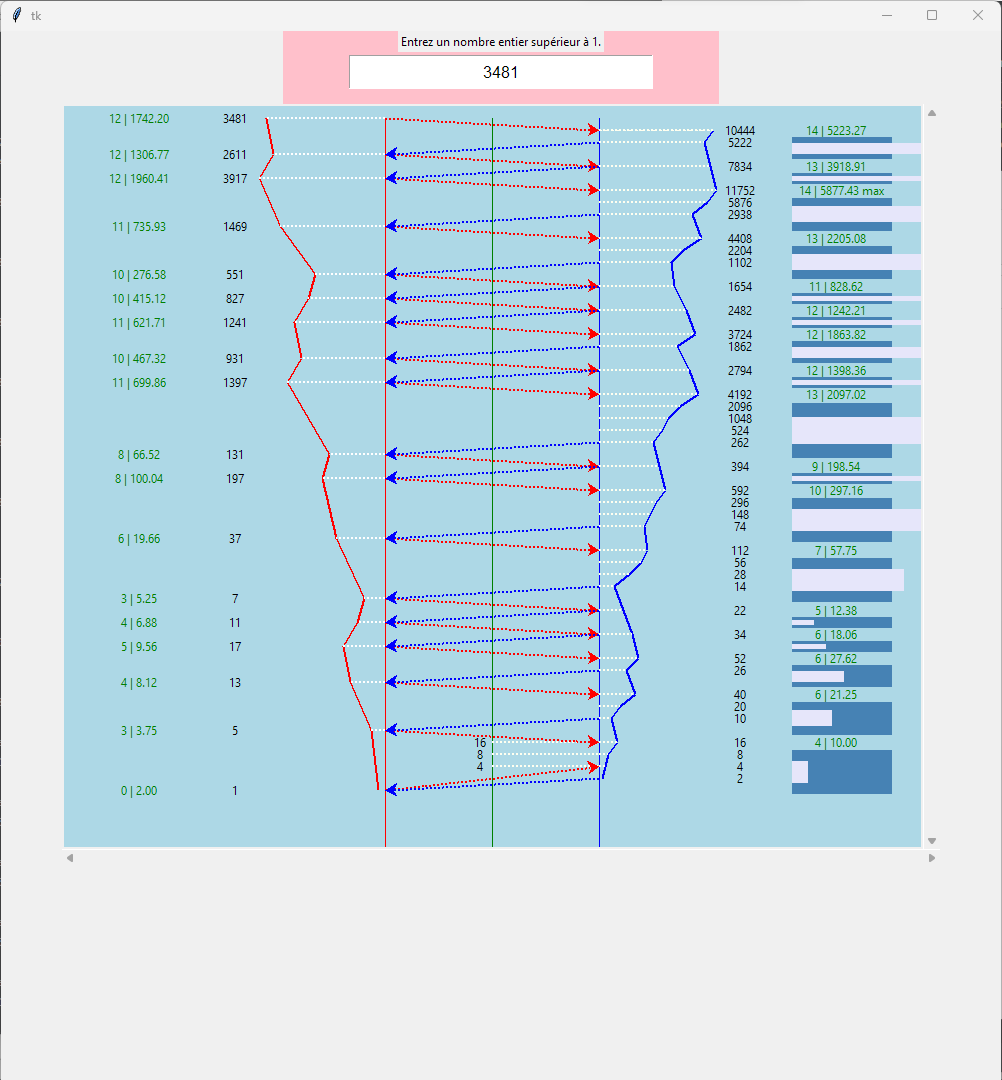
Nom : conjectCollatz3481.png
Affichages : 60
Taille : 60,2 Ko

Nom : conjectCollatz3481.png
Affichages : 60
Taille : 60,2 Ko

Bien qu'imparfaite, l'image reproduit le parcours des opérations..

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
 
# sve@ar lab's
"""Suivre la discussion avec Python ☺"""
 
 
# toumic : Car à chacun des nombres impairs l'opération (n*3+1) crée une ascendance
# (contrairement aux nombres pairs)._________________
""" sve@ar : (et le nombre d'opérations ayant amené ce résultat importe peu). """
#################################################################################################################
'''n3+1 remonte d'une section et n//2 peut descendre plusieurs sections'''
#################################################################################################################
# toumic : Les nombres pairs consécutifs, quand ils sont divisés par deux entrainent dans tous les cas un coup sur deux
# un nombre impair, (l'autre c'est qu'il est un nombre pair.
# Vous ne pouvez donc pas me contredire sans aucun exemple, ainsi vos réponses sont explicitement inappropriées
# et complètement négativistes, c'est votre droit
""" sve@ar : Aucun exemple. Juste moi je pars de 1024 et j'obtiens 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2 et 1 ;
    soit un impair et 10 pairs. C'est ça le "un coup sur deux" ??? """
# toumic : Essayez de partir du nombre 768 pour voir si liste_768[-1] = 2 ???
# Dico =  [768, 384, 192, 96, 48, 24, 12, 6]
n, t = (1024//2)+(1024//4), []
while not n%2:t.append(n);n //=2
("Liste Nombre pair t = ", t)
# Liste Nombre pair t =  [768, 384, 192, 96, 48, 24, 12, 6]
#################################################################################################################
#################################################################################################################
'''Pour résumer :
Vos raisonnements tant qu'ils ne distingueront pas les opérations (n/2) et (3n+1)..
D'un grand nombre unique donné parmi les sections liées aux nombres pairs !!
    Pour une liste contenant une série de nombres pairs :
        La liste_1024 = [1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1]
        La liste_l512 = [512, 256, 128, 64, 32, 16, 8, 4, 2, 1]
            § liste_1024[0] = liste_512[0]*2
    On peut sectionner la liste_n1024 en dix sous-ensembles pairs :
        La section_1024 = [max,,,min] =
            Max = section_1024[0] = 1024
            Min = section_1024[0]//2+2 (+2, pour s'échapper de l'autre section)
 
 
Déroulement de la section_512 (juste avant section_1024)
Pour 128 nombres pairs consécutifs de 258 à 512 :
    ♦ Le nombre 512 se dédouble 9 fois = 2**9 = 512.
    ♦ Le premier milieu 384 se dédouble 7 fois.
    ♦ La suite est simplifiée = (6*2),(5*4),(4*8),(3*16),(2*32),(1*64)
 
 
Déroulement de la section_128 (juste avant section_256)
Pour 32 nombres pairs consécutifs de 66 à 128 :
    ♦ Le nombre 128 se dédouble 7 fois = 2 ** 7 = 128.
    ♦ Le premier milieu 384 se dédouble 5 fois.
    ♦ Puis, (4*2), (3*4), (2*8), (1*16)
 
 
Déroulement de la section_64 (juste avant section_128)
Nombre à évaluer : 64
0=sans listes, 1=avec listes, 2=listes>1. Votre choix = 1
origine : 64 . Appartient à la section :  64
Dico =  [64, 32, 16, 8, 4, 2]                Longueur Terminale =  6
Dico =  [62]                  Longueur =  1
Dico =  [60, 30]                  Longueur =  2
Dico =  [58]                  Longueur =  1
Dico =  [56, 28, 14]                  Longueur =  3
Dico =  [54]                  Longueur =  1
Dico =  [52, 26]                  Longueur =  2
Dico =  [50]                  Longueur =  1
Dico =  [48, 24, 12, 6]                  Longueur =  4
Dico =  [46]                  Longueur =  1
Dico =  [44, 22]                  Longueur =  2
Dico =  [42]                  Longueur =  1
Dico =  [40, 20, 10]                  Longueur =  3
Dico =  [38]                  Longueur =  1
Dico =  [36, 18]                  Longueur =  2
Dico =  [34]                  Longueur =  1
 
 
 Résultats Globaux
Origine =  64 . Appartient à la section :  64
Longueur terminale =  6  = La l'exposant de 2
Nombre    listes =  16  = Le nombre total des listes
Partie    listes =  5  = Le nombre de parties trilog. Il reste =  0
Section   listes =  4  = La longueur de la plus grande sous-liste
'''

Je travaille à l'amélioration du programme de résolution et de définition

**wiztricks** · 29/06/2023, 18h19

Envoyé par Sve@r

Mais je crois que ce qui rend cette démonstration impossible c'est que cette suite n'en n'est pas une au sens mathématique. Une suite mathématique c'est une suite où tout terme Un+1 peut être calculé à partir des opérateurs mathématiques classiques (addition, soustraction, etc) appliqués sur le terme précédent Un.

L'article de wikipedia montre comment étendre cela aux nombres complexes.
Si on la limite aux entiers, lorsque le sinus de N demi-tours sera nul, le cosinus sera +/-1 et réciproquement (ils simplifient en prenant le carré). Donc on a une simple fonction f(n) et la suite est s_n = f(s_n-1).

- W

Résolution de la conjecture Collatz et problème de Syracuse

Téléchargez Python

Discussions similaires

Partager

Partager