Bonjour,
Je voudrais trouver un algorithme qui me permette de générer en automatique un championnat à plusieurs poules en optimisant les kilomètres parcourus par chaque équipe.
j'ai 30 équipes et je connais toutes les distances entre chaque équipes. Cela se passe sous forme de matchs A/R sur 18 dates : tout le monde se déplace chez tout le monde.
L'objectif est de faire 3 poules de 10 équipes en optimisant les kilomètres pour tout le monde.
Merci de me donner quelques pistes ...






 Répondre avec citation
Répondre avec citation









 dans tout ce qui précède !
dans tout ce qui précède !
 __
__
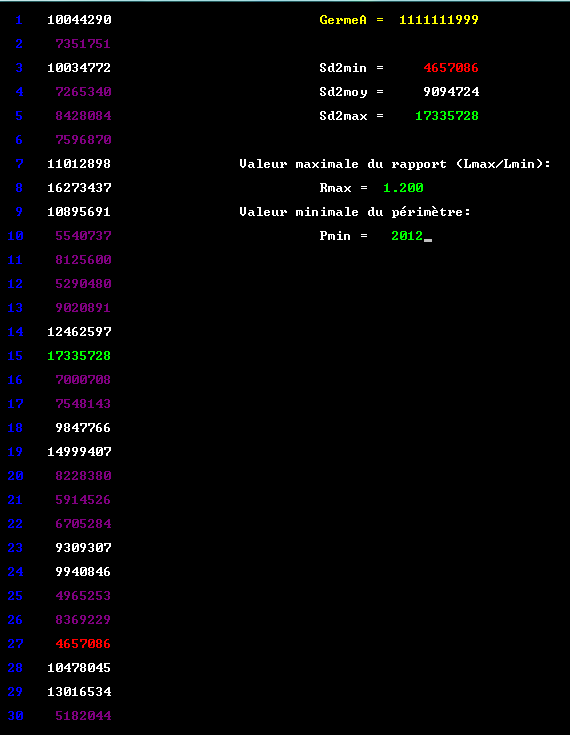
 __
__ __
__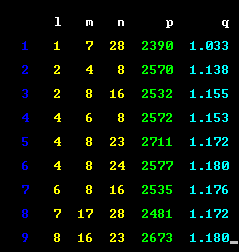 __
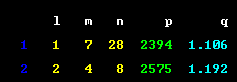
__

Partager