Quelques remarques :
1) Tu ne donnes pas la définition de R(n-1).
2) Au dénominateur, je vois e^(un truc). J'ai oublié le nom de cette lettre.... Pourrais-tu me redonner son nom ? 
Pourrais-tu aussi nous dire ce que vaut cette constante (ou cette fonction) ?
3) Pour commencer, je te conseille plutôt une récursivité simple. Tant pis tu recalcules plein de fois les mêmes. L'objectif est d'abord de faire une version qui marche avant de faire une version optimisée.
4) En continuité du point 4, je vois que tu as réécris pi^(-1/2) en 1/sqrt(pi). C'est juste (merci de me le rappeler, j'avais oublié cette égalité) mais cela éloigne ta fonction de la version originale et n'apporte probablement aucune optimisation pour ton code. Je te conseille dans un premier temps de faire une "bête" traduction de la formule.
5) Ton problème semble mal exposée. Tu dis par exemple :
Pour l'instant je me concentre sur la premiere integral qui se résume à l'estimation de cette somme:
Sauf que tu ne nous montres pas une somme, mais une fonction.
6) Au début de ton 2e code, je vois :
k1=10.0;to=5.5;Eimp=0.6;di=0.001;
Que viennent faire ces constantes ici ? A quoi correspondent-elles dans la formule montrée ? Voir le point 5 probablement.
7) Ton 2e code ne compile sans doute pas, car comme l'a dit stendhal666, tu ne peux pas utiliser psi comme une variable (lignes 23 et 26) puis comme une fonction (ligne 30), alors même que tu n'as pas définie de fonction double psi(int n) !
Pour l'amusement, j'ai commencé à coder cela en Python. Je sais que ce n'est pas le langage que tu utilises mais je te montre quand même comment j'ai structuré mon code :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| import math
n_max = 15
delta_t = 1.0 / n_max
toto = 1.0
Rn_1 = 1.0
print(n_max)
print(delta_t)
def psi(n):
print("psi({})".format(n))
# There is a common term between numerator and denominator
common = 4/3 * pow(math.pi, -1/2) * pow(delta_t, 1/2)
# Numerator contains a sum of previous psi for n in 1..n-1
sum_psi = 0
for i in range(1, n):
sum_psi += psi(i) * Rn_1
# Numerator and denominator
numerator = 1 + common + sum_psi
denominator = math.exp(-toto) + common
# Finally, return a fraction
return numerator / denominator
print(psi(5)) |
Comme tu peux le voir, je définie d'abord des constantes, puis une fonction pour calculer psi(n). Cette fonction est récursive, elle calcule les valeurs précédentes de psi(). Tu peux voir aussi que j'ai découpé le calcul de psi(n) en numérateur et dénominateur. J'ai aussi découpé ces 2 membres de mon opération pour plus de lisibilité, mais je suis resté sur la formule de départ, avec des exposant 1/2 plutôt qu'une racine carrée. Et comme tu vois, j'ai encore 2 termes que je ne connais pas : "toto" (la lettre que je ne connais plus...) et R(n-1).
PS : aurais-tu des valeurs exemples de psi(n) pour certaines valeurs de n, histoire qu'on puisse savoir si on calcule la bonne chose....
Bien joué Matt_Houston pour les 4/3 qu'il faut écrire 4.0/3.0 ! J'ai complètement omis dans mon code !
Résolution d'integrales avec variable variant dans la boucle
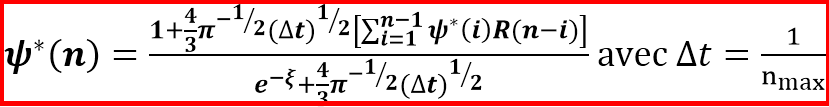
Répondre avec citation
Partager