par , 06/02/2023 à 09h25 (15757 Affichages)
I. Introduction
L'objectif de ce billet est de montrer comment tracer les différents appels d'une fonction récursive à l'aide de marqueurs placés dans le code de la fonction.
On va utiliser pour cela la librairie Python anytree qui va nous permettre de créer et de dessiner un arbre des appels.
Ce traçage des différents appels numérotés et regroupés par niveau sur un arbre permettra ainsi de mieux visualiser leur enchaînement et donc de mieux comprendre le mécanisme mis en œuvre.
Note importante : par la suite on prendra comme exemple la fonction récursive fibo(n) qui renvoie la valeur du nème terme de la suite de Fibonacci.
L'arbre des appels sera affiché sous forme de texte.
II. Module anytree
Il contient entre autre une classe Node permettant de créer une structure d'arbre classique et une autre classe RenderTree pour construire un itérateur et parcourir les nœuds de l'arbre.
II-A. Installation
Pour installer la librairie exécutez simplement la commande :
pip install anytree
II-B. Code exemple
On donne ici quelques lignes de code prises dans la documentation pour mieux comprendre comment utiliser anytree, et comment créer des objets Node ou RenderTree :
1
2
3
4
5
6
7
8
9
| >>> from anytree import Node, RenderTree
>>> udo = Node("Udo")
>>> marc = Node("Marc")
>>> lian = Node("Lian", parent=marc)
>>> print(RenderTree(udo))
Node('/Udo')
>>> print(RenderTree(marc))
Node('/Marc')
└── Node('/Marc/Lian') |
Par exemple, la ligne de code :
lian = Node("Lian", parent=marc)
Permet de créer le nœud enfant lian relié au nœud parent marc.
En l'absence de nœud parent, on crée alors simplement la racine de l'arbre.
Si vous souhaitez avoir plus d'information sur ce module je vous invite à consulter sa documentation.
III. Création de la classe ArbreAppels
Pour tracer les différents appels d'une fonction récursive, il nous faut créer une classe.
Notre classe ArbreAppels comportera un constructeur, c'est-à-dire une méthode particulière __init__() dont le code est exécuté quand la classe est instanciée.
Elle va nous permettre d'initialiser notre arbre et le compteur d'appel au moment de la création de l'objet :
1
2
3
4
5
6
| class ArbreAppels:
def __init__(self, nom_appel):
# initialisation des attributs de la classe
self.appel_courant = Node("1 -> " + nom_appel) # ajout de la racine (appel courant = appel n°1)
self.compteur_appel = 1 # initialisation du compteur d'appel
self.traceur_active = True # traçage activé par défaut |
Pour créer l'objet ArbreAppels avec le nom du 1er appel il suffit de faire :
1
2
| # création de l'objet ArbreAppels contenant la racine : 1er appel
arbre_appels = ArbreAppels("fibo(4)") |
III-A. Méthode ajouter_appel()
Pour ajouter des appels récursifs à notre arbre, nous devons en plus définir une méthode ajouter_appel() :
1
2
3
4
5
6
7
| class ArbreAppels:
...
def ajouter_appel(self, nom_appel):
if self.traceur_active: # si le traçage est activé
self.compteur_appel += 1 # incrémentation du compteur d'appel
nom_appel = str(self.compteur_appel) + " -> " + nom_appel # texte affiché sur le nœud, par exemple : "2 -> fibo(3)"
self.appel_courant = Node(nom_appel, parent = self.appel_courant) # ajout du nœud pour le nouvel appel |
Cette méthode permet donc de créer un nouvel objet Node à partir du nom du nœud et de son parent :
appel_enfant = Node("2 -> fibo(3)", parent=appel_parent)
Ajoutant ainsi un nœud à l'arbre des appels :

Ici on ajoute le nœud enfant correspondant à l'appel n°2 de la fonction fibo, au nœud parent correspondant à l'appel n°1.
Cette méthode peut être exécutée juste avant l'appel récursif :
1
2
3
4
5
6
7
8
9
| def fibo(n):
if n<=1: # si n=0 ou n=1
return n # retourne la valeur de n
else:
# ajout de l'appel fibo(n-1) à l'arbre des appels
arbre_appels.ajouter_appel("fibo(" + str(n-1) + ")")
fibo_n1 = fibo(n-1) # appel récursif : descente d'un niveau
... |
III-B. Méthode remonter_appel()
Pour remonter les appels dans notre arbre, nous devons aussi ajouter une méthode remonter_appel() :
1
2
3
4
5
6
| class ArbreAppels:
...
def remonter_appel(self):
if self.traceur_active: # si le traçage est activé
# on pointe désormais sur le nœud parent
self.appel_courant = self.appel_courant.parent |
Cette méthode permet donc de remonter d'un niveau dans l'arbre des appels :
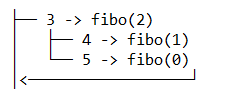
Ici on remonte d'un niveau : du nœud enfant 5 -> fibo(0) on passe au nœud parent 3 -> fibo(2).
Elle doit être exécutée juste après l'appel de la fonction récursive :
1
2
3
| ...
fibo_n1 = fibo(n-1) # appel récursif : descente d'un niveau
arbre_appels.remonter_appel() # remontée d'un niveau |
III-C. Méthode tracer()
Enfin, pour tracer les appels récursifs sur notre arbre, nous devons aussi ajouter une méthode tracer() qui permet de parcourir et d'afficher les nœuds de l'arbre :
1
2
3
4
5
6
| class ArbreAppels:
...
def tracer(self):
# parcours des nœuds de l'arbre depuis la racine
for pre, fill, node in RenderTree(self.get_racine()):
print("%s%s" % (pre, node.name)) # affiche le préfixe et le nom du nœud |
La fonction affiche un arbre des appels comme celui-ci :
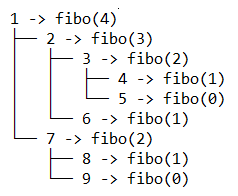
IV. Implémentation de l'arbre des appels
On souhaite maintenant tracer les différents appels récursifs d'une fonction à l'aide de la classe précédente.
Prenons comme exemple le calcul du nème terme de la suite de Fibonacci définie par la relation de récurrence :
Fi = Fi-1 + Fi-2
Avec comme premiers termes :
F0 = 0
F1 = 1
Partant de cette définition, on peut alors écrire une fonction récursive en Python qui évalue le nème terme de cette suite :
1
2
3
4
5
| def fib(n):
if n <= 1: # si 1er ou 2e terme : n=0 ou n=1
return n # retourne n
else: # sinon, appels récursifs basés sur la relation de récurrence
return fib(n-1) + fib(n-2) |
Considérons maintenant la variable arbre_appels faisant référence à un objet crée à partir de notre classe :
1
2
3
| # création de l'objet ArbreAppels contenant la racine : 1er appel
arbre_appels = ArbreAppels("fibo(4)")
... |
On peut alors positionner les marqueurs de début et de fin des appels aux bons endroits dans le code :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| def fibo(n):
if n<=1: # si n=0 ou n=1
return n # retourne la valeur de n
else:
# ajout de l'appel fibo(n-1) à l'arbre des appels
arbre_appels.ajouter_appel("fibo(" + str(n-1) + ")")
fibo_n1 = fibo(n-1) # appel récursif : descente d'un niveau
arbre_appels.remonter_appel() # remontée d'un niveau dans l'arbre
# ajout de l'appel fibo(n-2) à l'arbre des appels
arbre_appels.ajouter_appel("fibo(" + str(n-2) + ")")
fibo_n2 = fibo(n-2) # appel récursif : descente d'un niveau
arbre_appels.remonter_appel() # remontée d'un niveau dans l'arbre
return (fibo_n1 + fibo_n2) # sortie |
Note importante : comme l'instruction return provoque la sortie immédiate de la fonction, si le marqueur indiquant la remontée des appels est positionné juste après un return, il ne sera pas pris en compte.
De plus, on constate que la variable arbre_appels est déclarée à l'extérieur de la fonction fibo. En effet, on peut toujours ensuite faire référence à cette variable dans la fonction si on ne modifie pas sa valeur.
On peut également ajouter une gestion des exceptions à la fonction pour désactiver le traçage des appels dans le cas où une exception est levée :
1
2
3
4
5
6
7
8
9
10
11
| def fibo(n):
try:
# code de la fonction
except Exception as e: # si une exception est levée
if arbre_appels.traceur_active: # si le traçage est activé
# on désactive le traçage des appels
arbre_appels.traceur_active=False
# on affiche le message d'erreur
print(e)
return False |
Testons maintenant notre fonction :
1
2
3
4
5
6
7
8
| # création de l'objet ArbreAppels contenant la racine : 1er appel
arbre_appels = ArbreAppels("fibo(4)")
# exécute la fonction pour n=4
fibo_n = fibo(4)
# trace l'arbre des appels
arbre_appels.tracer() |
Le code affiche :

Module complet de test :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| from anytree import Node, RenderTree
class ArbreAppels:
def __init__(self, nom_appel):
# initialisation des attributs de la classe
self.appel_courant = Node("1 -> " + nom_appel) # ajout de la racine (appel courant = appel n°1)
self.compteur_appel = 1 # initialisation du compteur d'appel
self.traceur_active = True # traçage activé par défaut
def ajouter_appel(self, nom_appel):
if self.traceur_active: # si le traçage est activé
self.compteur_appel += 1 # incrémentation du compteur d'appel
nom_appel = str(self.compteur_appel) + " -> " + nom_appel # texte affiché sur le nœud, par exemple : "2 -> fibo(3)"
self.appel_courant = Node(nom_appel, parent = self.appel_courant) # ajout du nœud pour le nouvel appel
def remonter_appel(self):
if self.traceur_active: # si le traçage est activé
# on pointe désormais sur le nœud parent
self.appel_courant = self.appel_courant.parent
def get_racine(self):
# on renvoie la racine de l'arbre
return self.appel_courant.root
def tracer(self):
# parcours des nœuds de l'arbre depuis la racine
for pre, fill, node in RenderTree(self.get_racine()):
print("%s%s" % (pre, node.name)) # affiche le préfixe et le nom du nœud
def fibo(n):
try:
if n<=1: # si n=0 ou n=1
return n # retourne la valeur de n
else:
# ajout de l'appel fibo(n-1) à l'arbre des appels
arbre_appels.ajouter_appel("fibo(" + str(n-1) + ")")
fibo_n1 = fibo(n-1) # appel récursif : descente d'un niveau
arbre_appels.remonter_appel() # remontée d'un niveau dans l'arbre
# ajout de l'appel fibo(n-2) à l'arbre des appels
arbre_appels.ajouter_appel("fibo(" + str(n-2) + ")")
fibo_n2 = fibo(n-2) # appel récursif : descente d'un niveau
arbre_appels.remonter_appel() # remontée d'un niveau dans l'arbre
return (fibo_n1 + fibo_n2) # sortie
except Exception as e: # si une exception est levée
if arbre_appels.traceur_active: # si le traçage est activé
# on désactive le traçage des appels
arbre_appels.traceur_active=False
# on affiche le message d'erreur
print(e)
return False # sortie de l'appel récursif
# création de l'objet ArbreAppels contenant la racine : 1er appel
arbre_appels = ArbreAppels("fibo(4)")
# exécute la fonction pour n=4
fibo_n = fibo(4)
# trace l'arbre des appels
arbre_appels.tracer() |
V. Conclusion
Après avoir présenté la librairie anytree, nous avons montré comment créer notre classe ArbreAppels à l'aide de ce module.
Enfin, nous avons donné un exemple d'utilisation de cette classe pour tracer les différents appels récursifs de la fonction fibo(n).
Sources
https://anytree.readthedocs.io/en/latest/
https://fr.wikipedia.org/wiki/Suite_de_Fibonacci











