par , 02/07/2021 à 10h13 (6637 Affichages)
I. Introduction
En pratique, il est souvent utile pour améliorer l'efficacité d'un algorithme mathématique de mémoriser la valeur d'une expression à l'indice i, pour ensuite l'utiliser pour calculer sa valeur à l'indice i+1. Pour cela, on cherche à établir une relation de récurrence entre 2 termes consécutifs.
II. Algorithme de calcul de l'exponentiel de x
Le développement en série de ex s'écrit
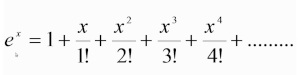
En posant :
ai=xi/i!
On peut aussi écrire :
ex = a0 + a1 + a2 + ... + ai + .. .
Pour éviter d'avoir à calculer entièrement chaque terme de la série, on va donc chercher à établir une relation entre 2 termes consécutifs.
En comparant les 2 séries, on peut facilement établir une relation de récurrence permettant de passer du terme ai-1 à ai :
ai = (x/i)*ai-1
Le code permettant le calcul des n+1 premiers termes du développement peut alors s'écrire :
1
2
3
4
5
| s=1 : a=1 ' initialisation des variables
for i=1 to n ' on parcourt les indices des termes jusqu'à n
a= a*(x/i) ' calcul de la valeur du terme d'indice i
s = s + a ' ajout de sa valeur à la somme
next i ' prochain indice |
Une seule boucle au lieu de 2 imbriquées.
III. Polynômes de Lagrange
En analyse numérique, les polynômes de Lagrange permettent d'interpoler une série de points par un polynôme qui passe exactement par ces points.
Dans une interpolation lagrangienne on construit un polynôme de degré n à partir d'une série de n+1 points (X0,y0),(X1,Y1),...,(Xn,Yn) :
En supposant ici que les valeurs X0,X1,x2,...,Xn sont également espacées d'un intervalle h, ce qui n'est malheureusement pas toujours le cas, on va chercher à optimiser l'efficacité de l'algorithme d'interpolation des n+1 points, en identifiant à nouveau une relation de récurrence entre les polynômes de Lagrange.
Brève présentation de la formule du polynôme d'interpolation :
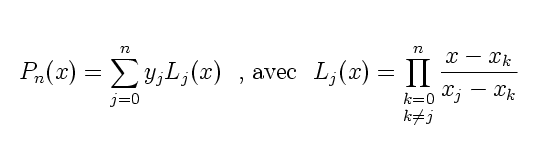
Ce qui donne en VBA :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| Public Function Pn(Xi As Variant, Yi As Variant, X As Double) As Double
' évalue le polynôme d'interpolation pour la série de points (Xi,Yi) et pour la valeur d'abscisse X
Dim Lx As Double ' variable contenant la valeur du polynôme de Lagrange
Dim i As Long, j As Long ' variables d'indices pour les X et Y
For i = 0 To UBound(Yi) ' parcourt des indices des Y
Lx = 1 ' on initialise la variable
' évaluation du polynôme de Lagrange d'indice i
For j = 0 To UBound(Xi) ' parcourt des indices des X
If j <> i Then
Lx = Lx * ((X - Xi(j)) / (Xi(i) - Xi(j))) ' on évalue de polynôme de Lagrange
End If
Next j
Pn = Pn + Lx * Yi(i) ' on évalue de polynôme d'interpolation
Next i
End Function |
On peut déjà constater que les polynômes Li(X) doivent être entièrement recalculés pour chaque indice i, ce qui est coûteux en terme de temps d'exécution.
N'y aurait-il pas moyen, comme dans le 1er exemple, d'utiliser la valeur du polynôme d'indice (i-1), pour obtenir directement celle du polynôme d'indice i ?
Pour n=3 on a le tableau des polynômes de Lagrange :

On va donc essayer de trouver une expression permettant de passer directement de Li-1(X) à Li(X), et ainsi obtenir un nombre total d'opérations algébriques proportionnel au nombre de valeurs.
En supposant que l'intervalle h entre 2 valeurs consécutives est constant, on peut évaluer les écarts entre ces valeurs en fonction de h :
| X0 - X1 |
X0 - X2 |
... |
X1 - X2 |
X1 - X3 |
... |
Xi - Xj |
... |
| -h |
-2h |
... |
-h |
-2h |
... |
(i-j)*h |
... |
Après avoir exprimé certains écarts en fonction de h sur les 2 premières lignes, notre tableau de polynômes devient :

On voit bien que dans le cas général on passe de Li-1(X) à Li(X) grâce à la formule :
Li(X) = Li-1(X) * ((X - Xi-1) / (X - Xi)) * ((Xi-1 - Xn) / (Xi - X0)).
Ou sous une autre forme :
Li(U) = Li-1(U) * ((U - (i - 1)) / (U - i)) * ((i - 1 - n) / i) avec le changement de variables U = (X - X0) / h.
Et pour évaluer le polynôme d'interpolation, connaissant L0, on peut donc utiliser une seule boucle :
1
2
3
4
| For i = 1 To n 'on parcourt les indices des X
Lx = Lx * ((X - Xi(i - 1)) / (X - Xi(i))) * ((Xi(i - 1) - Xi(n)) / (Xi(i) - Xi(0))) ' calcul du polynôme de Lagrange d'indice i
Pn = Pn + Lx * Yi(i) ' ajout au polynôme d'interpolation
Next i ' prochain indice |
La fonction d'évaluation du polynôme s'écrit alors :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| Public Function Pn2(Xi() As Double, Yi() As Double, X As Double) As Double
' évalue le polynôme d'interpolation pour la série de points (Xi,Yi) et pour la valeur d'abscisse X
On Error GoTo err_Ph2
Dim n As Long, Lx As Double
Dim i As Long ' variable d'indices pour les X
n = UBound(Xi) ' indice de la plus grande valeurs pour les X
Lx = 1 ' initialisation du polynôme de Lagrange
' évaluation du polynôme de Lagrange d'indice 0
For i = 1 To n ' on parcourt les indices des n valeurs suivant la 1ère
Lx = Lx * ((X - Xi(i)) / (Xi(0) - Xi(i))) ' on met à jour la variable Lx
Next i
Pn2 = Pn2 + Lx * Yi(0) ' ajout de la valeur de Lx au polynôme d'interpolation
For i = 1 To n ' on parcourt les indices des valeurs de X
Lx = Lx * ((X - Xi(i - 1)) / (X - Xi(i))) * ((Xi(i - 1) - Xi(n)) / (Xi(i) - Xi(0))) ' évaluation du polynôme de Lagrange d'indice i
Pn2 = Pn2 + Lx * Yi(i) ' ajout de la valeur de Lx au polynôme d'interpolation
Next i
err_Ph2:
If Err.Number = 11 Then ' dans le cas ou on a une division par zéro : la valeur de X est égale à la valeur de Xi(i)
Pn2 = Yi(i) ' on renvoie la valeur de Y correspondante
End If
End Function |
Les indices des tableaux de valeurs Xi() et Yi() commencent à 0.
La gestion d'erreur permet de renvoyer directement la valeur de Yi dans le cas où la valeur X passée à la fonction est égale à Xi. L'erreur provoquée par la division par 0 à l'indice i est alors interceptée puis traitée en renvoyant la valeur de Yi.
IV. Conclusion
Ayant posé comme contrainte que l'écart entre 2 valeurs consécutives de X est constant, et après avoir identifié une relation de récurrence entre 2 termes successifs du polynôme d'interpolation, nous avons pu écrire une fonction dont le temps d'exécution est nettement plus court que pour la version classique.
Attention toutefois, car l'expression du polynôme d'interpolation peut engendrer une instabilité numérique, notamment lorsque le nombre de points et donc le degré du polynôme devient relativement important. Il vaut mieux dans ce cas décomposer l'échantillon des points en sous-ensembles plus petits, mais tout ceci dépasse largement le cadre de ce billet.










