Intersection entre 2 cercles

**kingja** · 29/04/2021, 19h49

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
 
function AreCirclesIntersecting(c0,c1) {
 
    x0 = c0['center']['x'];
    y0 = c0['center']['y'];
    r0 = c0['center']['r'];
    x1 = c1['center']['x'];
    y1 = c1['center']['y'];
    r1 = c1['center']['r'];
 
 
    var a, dx, dy, d, h, rx, ry;
    var x2, y2;
 
    /* dx and dy are the vertical and horizontal distances between
     * the circle centers.
     */
    dx = x1 - x0;
    dy = y1 - y0;
 
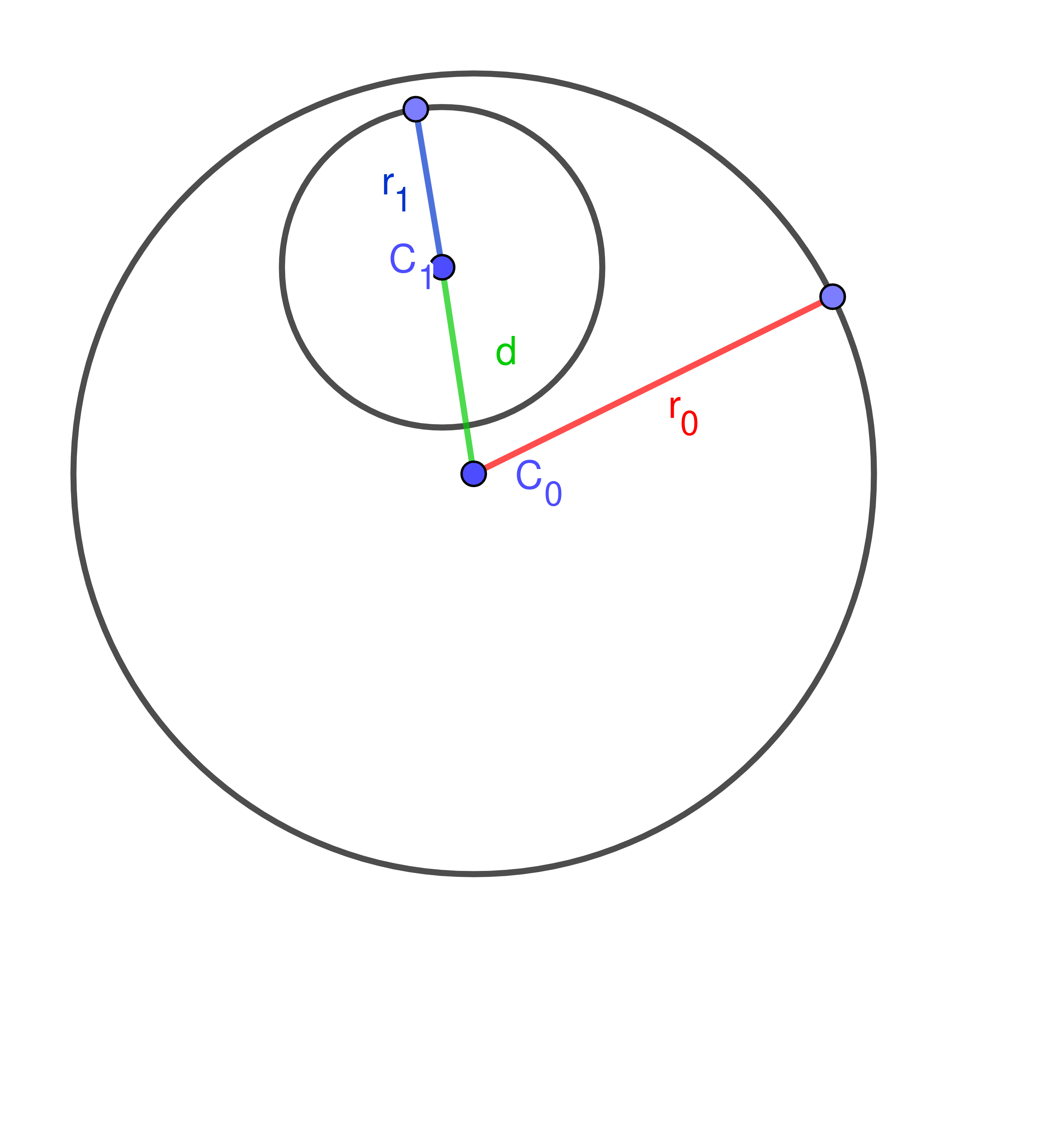
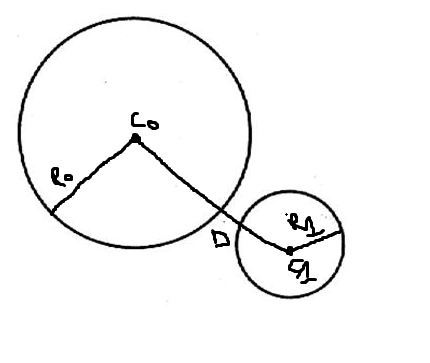
    /* Determine the straight-line distance between the centers. */
    d = Math.sqrt((dy*dy) + (dx*dx));
 
    /* Check for solvability. */
    if (d > (r0 + r1)) {
        /* no solution. circles do not intersect. */
        return false;
    }
    if (d < Math.abs(r0 - r1)) {
        /* no solution. one circle is contained in the other */
        return false;
    }
 
    /* 'point 2' is the point where the line through the circle
     * intersection points crosses the line between the circle
     * centers.  
     */
 
    /* Determine the distance from point 0 to point 2. */
    a = ((r0*r0) - (r1*r1) + (d*d)) / (2.0 * d) ;
 
    /* Determine the coordinates of point 2. */
    x2 = x0 + (dx * a/d);
    y2 = y0 + (dy * a/d);
 
    /* Determine the distance from point 2 to either of the
     * intersection points.
     */
    h = Math.sqrt((r0*r0) - (a*a));
 
    /* Now determine the offsets of the intersection points from
     * point 2.
     */
    rx = -dy * (h/d);
    ry = dx * (h/d);
 
    /* Determine the absolute intersection points. */
    var xi = x2 + rx;
    var xi_prime = x2 - rx;
    var yi = y2 + ry;
    var yi_prime = y2 - ry;
 
    return [xi, xi_prime, yi, yi_prime];
 
}
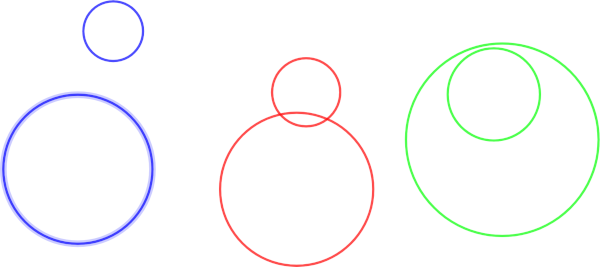
const circles = [
    {center: {x: 10.0, y: 10.0}, radius: 5.0},
    {center: {x: 20.0, y: 20.0}, radius: 15.0},
    {center: {x: 20.0, y: 10.0}, radius: 5.0},
    {center: {x: 20.0, y: 25.0}, radius: 7.5},
];
 
const q7_result1 = AreCirclesIntersecting(circles[0], circles[1]);
console.log(q7_result1); // Expected output: true
 
const q7_result2 = AreCirclesIntersecting(circles[0], circles[2]);
console.log(q7_result2); // Expected output: true
 
const q7_result3 = AreCirclesIntersecting(circles[1], circles[3]);
console.log(q7_result3); // Expected output: false
 
const q7_result4 = AreCirclesIntersecting(circles[2], circles[3]);
console.log(q7_result4); // Expected output: false

Salut, j'essaye de faire une fonction pour détecter des intersections entre 2 cercles. Si oui il marque true, sinon il marque false, Mais je crois bien que je me suis perdu du coup il n'affiche ce que je veux. Si quelqu'un peut bien m'aider svp . Merci

**mathieu** · 29/04/2021, 21h11

nous ne connaissons pas les équations qui vous ont amené a faire ce code. donc le plus rapide est que vous débuguiez en affichant le contenu des variables.

**WhiteCrow** · 29/04/2021, 22h02

D'autant plus que s'il ne s'agit que de renvoyer true ou false suivant qu'il y ait ou non une intersection c'est simple :

cas 1 : un cercle dans l'autre → si distance entre les centres + le plus petit rayon < plus grand rayon → renvoyer false
cas 2 : cercles disjoints et extérieurs l'un à l'autre → si distance entre les centre > somme rayons → renvoyer false
cas 3 : cercles non disjoints → dans tous les autres cas → renvoyer true

Il suffit de faire un dessin.

**kingja** · 29/04/2021, 22h18

Donc si j'ai bien compris les deux cas false se résumerait comme ca ?

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
if (d > (r0 + r1)) {
        /* no solution. circles do not intersect. */
        return false;
    }
    if (d < Math.abs(r0 - r1)) {
        /* no solution. one circle is contained in the other */
        return false;
    }

**WhiteCrow** · 29/04/2021, 22h36

fais un dessin et cela te paraîtra évident.

Par exemple pour le cas 1 : Nom : cas1.png
Affichages : 488
Taille : 376,7 Ko

Tu vois bien que si d (la distance entre les centres) + r1 (le plus petit des deux rayons) est strictement inférieur à r0 (le plus grand des deux rayons) alors il n'y a pas d'intersection.
Fais des dessins pour le cas 2 et quelques dessins pour les autres cas … et tu comprendras très vite.

Le trick de la valeur absolu fonctionne évidemment … mais vois-tu pourquoi ?

**kingja** · 29/04/2021, 22h50

non justement , d'ailleurs c'est pour ca que je me suis perdu . ET je me suis demandé si les quatre dernières lignes de la fonction était nécessaire ?

**WhiteCrow** · 29/04/2021, 23h01

écris ta propre fonction, n'essaye pas d'en prendre une et de l'adapter alors que tu n'y comprends pas grand chose.
C'est un exo facile, fais les dessins … tu verras. Tu as tout en main.

**kingja** · 29/04/2021, 23h10

Nom : Capture.PNG
Affichages : 419
Taille : 21,1 Ko

le deuxième cas ressemble à ça ?

**WhiteCrow** · 29/04/2021, 23h13

Envoyé par WhiteCrow

[...]

cas 2 : cercles disjoints et extérieurs l'un à l'autre → si distance entre les centre > somme rayons → renvoyer false

[...]

Non, cercles disjoints ( = qui ne se coupent pas ) et extérieurs l'un à l'autre ( = un n'est pas dans l'autre ) …

**kingja** · 29/04/2021, 23h21

Nom : &.PNG
Affichages : 399
Taille : 26,0 Ko

Ok d'accord donc c'est comme ca ?

la commence a être clair du coup le code des conditions devraient ressembler à ça ?

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
 if (d +r1 < r0 )
       {
        return false;
       }
    if (d > (r0 + r1) 
      {
        return false;
      }

**WhiteCrow** · 30/04/2021, 06h22

ça commence à ressembler à quelque chose (à l'indentation près). Mais n'essaye pas de le faire tomber en marche par hasard ou par tâtonnements … Il faut comprendre ce que tu veux faire (notre discussion), comment tu peux le faire (mon premier message qui te donnait tout) et comment tu l'implémentes …

Envoyé par WhiteCrow

D'autant plus que s'il ne s'agit que de renvoyer true ou false suivant qu'il y ait ou non une intersection c'est simple :

cas 1 : un cercle dans l'autre → si distance entre les centres + le plus petit rayon < plus grand rayon → renvoyer false
cas 2 : cercles disjoints et extérieurs l'un à l'autre → si distance entre les centre > somme rayons → renvoyer false
cas 3 : cercles non disjoints → dans tous les autres cas → renvoyer true

Il suffit de faire un dessin.

Dans le cas 1 il y a les mots plus petit et plus grand … je ne les vois pas dans ton code.

Si tu fais un dessin pour le cas 3, peux-tu constater qu'effectivement on n'est ni dans le cas 2 ni dans le cas 1 ?

**SpaceFrog** · 30/04/2021, 08h35

https://www.geeksforgeeks.org/distan...ngth-is-given/
https://stackoverflow.com/questions/...section-points

**kingja** · 30/04/2021, 11h08

Envoyé par SpaceFrog

https://www.geeksforgeeks.org/distan...ngth-is-given/
https://stackoverflow.com/questions/...section-points

Merci beaucoup , je crois que j'ai quasiment tous fais de la même façon ? a moins que je me sois trompé en quelque part mais justement je sais pas ou.

**kingja** · 30/04/2021, 11h11

Envoyé par WhiteCrow

ça commence à ressembler à quelque chose (à l'indentation près). Mais n'essaye pas de le faire tomber en marche par hasard ou par tâtonnements … Il faut comprendre ce que tu veux faire (notre discussion), comment tu peux le faire (mon premier message qui te donnait tout) et comment tu l'implémentes …

Dans le cas 1 il y a les mots plus petit et plus grand … je ne les vois pas dans ton code.

Si tu fais un dessin pour le cas 3, peux-tu constater qu'effectivement on n'est ni dans le cas 2 ni dans le cas 1 ?

plus petit et plus grand ne serait pas ro et r1 ? et pour le 3ème cas : Si d = 0 et r 0 = r 1 alors les cercles coïncident ? Mais je vois pas trop comment le faire en dessin par contre

**WhiteCrow** · 30/04/2021, 11h51

Bah non, a priori tu ne sais pas lequel des deux cercles passés en paramètres est celui de plus grand rayon …
Les trois cas de figures :
Nom : 3_cas.png
Affichages : 440
Taille : 35,8 Ko

Nom : 3_cas.png
Affichages : 440
Taille : 35,8 Ko

Le cas bleu est ce que j'ai appelé le cas 2, le cas rouge est le cas 3 et le cas vert est le cas 1.
Ajoute les rayons, détermine les tests … pour obtenir les minimum m de deux nombres a et b → m=Math.min(a,b) ; pour le max la fonction est Math.max.