Discussion :

[mmsoaihua]

Bonjour à tous !

J'essaye d'apprendre les algorithmes basiques, malheureusement je me casse la tête et je n’avance pas avec le crible d'Ératosthène.. Il me semble que le premier algorithme écrit dans python as une faute logique.

Code python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
def er_sieve(n):
      sieve = [1] * (n+1); sieve[0] = sieve[1] = 0
      for i in range(2, int(n**.5)+1):
        if not sieve[i]: continue
        for j in range(i*2, n+1, i): sieve[j] = 0
      prime_numbers = [i for i in range(2, n+1) if sieve[i]]
      return sieve, prime_numbers

Code cpp :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Deuxieme: 
// 素数列挙
// nまでの素数をEratosthenesの篩で列挙する
// 計算量O(nloglogn)
template<class T>
vector<T> prime_list(T n){
    vector<T> ret;
    vector<T> isPrime(n+1,1);
    isPrime[0] = isPrime[1] = 0;
    for(long long i = 2; i <= n; ++i){
        if(isPrime[i] == 0) continue;
        ret.push_back(i);
        for(long long j = i*i; j <= n; j += i) isPrime[j] = 0;
    }
    return ret;
    // return isPrime;  // 状況によってはこっちを返す
}

Est-ce que les deux algorithmes sont bien écrit? Dans le deuxieme il y a for(j = i*i; j <= j += 1),
mais dans le premièr for j in range(i*2, n+1, i)?!!?!
Merci bien pour votre temps!

[laurent_ott]

Bonjour.
Je ne connais pas Python donc je ne peux pas apporter de réponse à vos questions.
Mais je me permets de vous rappeler le principe du crible d'Ératosthène au cas où ça peut vous aider :
imaginez une grille numérotée de 1 à 100. Partez du nombre 2 et rayez les nombres suivants en avançant de 2 en 2 : c'est-à-dire les nombres 4, 6, 8, 10, 12, etc. Puis partez du nombre 3 et rayez les nombres suivants en avançant de 3 en 3 : les nombres 6, 9, 12, 15, 18, etc. Partez du nombre 4 et rayez les nombres suivants en avançant de 4 en 4 : 8, 12, 16, etc.
En répétant la manipulation jusqu'au nombre 7, vous obtenez cette grille où les nombres qui ne sont pas rayés (ici en orange) donnent la liste des nombres premiers jusqu'à 100 (hormis le 1 qui n'est pas un nombre premier).



Bonne continuation.

[Nebulix]

Cette discussion répond de façon intéressante à la discussion sur les langages d'initiation à l'informatique
(https://www.developpez.net/forums/d2...-informatique/)
Tes exemples de code sont tellement peu lisibles que tu ne t'y retrouves pas toi même.
Il est facile de traduire quasi littéralement en Pascal l'algoritme donné par laurent_ott ...

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const n=100;
var prime:array[1..n]of boolean;
procedure TForm1.Button1Click(Sender: TObject);//celle qui fait le boulot
var i,j,k,m:integer;
begin
//initialisations
for i:=1 to n do prime[i]:=true;
prime[1]:=false;
m:=trunc(sqrt(n))+1;
//calcul
for i:= 1 to m do if prime[i] then begin
  j:=i;
  while j<=n do begin
    j:=j+i;
    prime[j]:=false;
    end ;
  end;
for i:= 1 to 100 do if prime[i] then memo1.lines.add(inttostr(i));//visu des résultats
end;

[dourouc05]

Tes exemples de code sont tellement peu lisibles que tu ne t'y retrouves pas toi même.

Ah bon ? En quoi ce code Pascal est-il plus lisible ? Il a surtout l'énorme "avantage" de mêler des notions de GUI avec de l'algorithmique… Sans oublier une jolie ligne qui contient une boucle, une condition, puis une instruction. Il ne faut pas confondre incompétence de la personne qui pose une question avec ton incompétence en Python ou en C++ ou avec tes goûts en termes de langage de programmation…

Pour le code Python, j'ai retouché la présentation et remplacé l'utilisation d'entiers par des booléens (vu que ce sont des valeurs binaires et non entières). Ça semble marcher :

Code python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
def er_sieve(n):
	sieve = [True] * (n+1)
	sieve[0] = False
	sieve[1] = False
 
	for i in range(2, int(n**.5)+1):
		if not sieve[i]: 
			continue
		for j in range(i*2, n+1, i): 
			sieve[j] = False
 
	prime_numbers = [i for i in range(2, n+1) if sieve[i]]
	return prime_numbers

Aurais-tu des cas où tu n'obtiens pas les résultats attendus ?

Pour le code C++, la même modification s'applique : isPrime devrait être un vecteur de booléens (ce qui prendrait au moins soixante-quatre fois moins de mémoire sur une machine 64 bits). Les deux boucles sont bien équivalente, renseigne-toi sur l'utilisation de range() en Python (https://docs.python.org/3.8/library/...es.html#ranges) : partir de 2i (puisqu'on vient de marquer i comme premier, son premier multiple est 2i) ; incrémenter par pas de i (donc passer sur tous les multiples) ; aller jusqu'à la fin des nombres à considérer (n).
La grande différence est en termes d'efficacité (même si ça ne devrait pas changer grand-chose à la complexité asymptotique), c'est que le code Python ne considère des nombres premiers que jusque au lieu de n. Je ne pense pas que ça change grand-chose en termes de correction.

[Pyramidev]

Bonjour,

Voici un code lisible en Python avec les tests unitaires, dont les doctests :

Code Python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import doctest
from math import sqrt
import sys
import unittest
 
 
def sieve_of_eratosthenes(n):
    """
    Return the prime numbers from 2 to n.
 
    Algorithm: sieve of Eratosthenes
    https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
 
    >>> sieve_of_eratosthenes(10)
    [2, 3, 5, 7]
    >>> sieve_of_eratosthenes(11)
    [2, 3, 5, 7, 11]
    """
    assert isinstance(n, int)
    assert n >= 1
    primeness_list = [False, False] + [True] * (n - 1)
    for number in range(2, int(sqrt(n)) + 1):
        the_number_is_prime = primeness_list[number]
        if not the_number_is_prime:
            continue
        for multiple_of_number in range(number*2, n+1, number):
            primeness_list[multiple_of_number] = False
    return [number for number, is_prime in enumerate(primeness_list) if is_prime]
 
 
class Test(unittest.TestCase):
    def test(self):
        self.assertEqual(sieve_of_eratosthenes(1), [])
        self.assertEqual(sieve_of_eratosthenes(2), [2])
        self.assertEqual(
            sieve_of_eratosthenes(100),
            [
                2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
                53, 59, 61, 67, 71, 73, 79, 83, 89, 97
            ]
        )
 
if __name__ == "__main__":
    failure_count, _ = doctest.testmod()
    if failure_count != 0:
        sys.exit(1)
    unittest.main()

[Pyramidev]

dourouc05 avait déjà répondu sur la plupart des points importants et j'avais publié mon précédent message un peu trop vite.

Nebulix, j'aimerais bien savoir ce que tu trouves illisible en Python par rapport à du Pascal.

• n**.5 n'est pas joli, mais ce n'est pas la manière idiomatique en Python de calculer une racine carrée. En Python, on peut aussi écrire sqrt(n).
• En Python, quand on connaît le comportement de range, range(number*2, n+1, number) est plus direct que ta boucle while en Pascal. D'ailleurs, on pourrait aussi utiliser while en Python, mais ce serait moins idiomatique dans le cas présent.
• S'il s'agit des déclarations de type, on peut en faire en Python aussi et les vérifier avec un analyseur de typage statique. Par exemple, dans mon code, j'aurais pu aussi annoter la fonction ainsi : def sieve_of_eratosthenes(n: int) -> List[int]:. Cela pourrait être utile dans un plus gros programme pour vérifier le typage dans le code appelant. Mais bon, là, il s'agit d'un simple exercice. Le doctest et les autres tests unitaires illustrent déjà ce que la fonction prend en paramètre et retourne.

[Nebulix]

D'abord merci de montrer qu'on peut débattre sans insulter. Je n'avais comme but que d'aider mmsoaihua, et je trouve navrant d'avoir le genre de réponse qu'a fait dourouc.
Le problème n'est pas ce que je trouve illisible, mais ce que mmsoaihua trouve illisible ou a fortiori ce qu'un débutant trouve illisible. Le but n'étant pas de faire un exercice de langage mais de coder de la manière la plus fiable un algorithme. Je parle de ma propre expérience.
Si un algorithme est donné en langage naturel, il est beaucoup plus fiable de la transcrire dans un langage informatique proche du langage naturel. La forme for i:=1 to n me semble un peu plus évidente que for i in range[1,n] même si on voit vite que c'est pareil. Et comme tu écris : "En Python, quand on connaît le comportement de..." cela signifie bien que ce n'est pas forcément évident. Et des lignes de code telles que :

Code Python :

Sélectionner tout - Visualiser dans une fenêtre à part

return [number for number, is_prime in enumerate(primeness_list) if is_prime]

ou

Code Python :

Sélectionner tout - Visualiser dans une fenêtre à part

prime_numbers = [i for i in range(2, n+1) if sieve[i]]

semblent demander un minimum d'expertise ...
Quand j'étais étudiant, j'ai failli rater un examen parce que je n'avais pas noté que Fortran IMPLICITEMENT considérait comme entier des variables commençant par i,j,k...J'en ai gardé une méfiance farouche envers tout ce qui est implicite. D'ailleurs tu sembles d'accord.
P.S. J'ai fait une erreur ligne 11 en écrivant n au lieu de m défini juste au-dessus. Il y a peut-être des techniques pour éviter çà ...

[laurent_ott]

Bonjour.
Lors de mon premier message, je me contentais de rappeler le principe du crible d’Ératosthène.
Il est évident qu'il est possible de faire des améliorations lors d'une programmation, car les colonnes pairs ne sont jamais des premiers, idem pour la colonne des 5, sauf le nombre 5.
Ce qui pourrait donner le code suivant (en Basic) :

Code VB :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
'-------------------------------------------------------------------------------
Sub Eratosthene(n As Long)
'-------------------------------------------------------------------------------
' Retourne la liste des nombres premiers jusqu'à n.
'-------------------------------------------------------------------------------
Dim i As Long, j As Long, y As Long, c As Integer
Dim Nombre() As Byte
 
' Variable qui va contenir tout le tableau des nombres:
ReDim Nombre(1 To n)
 
' Boucle sur les colonnes de 2 en 2 pour évincer les colonnes impaires:
c = -2
For i = 3 To Sqr(n) Step 2
    c = c + 1
    ' Ne pas traiter la colonne des 5:
    If c = 5 Then
        c = 0
    Else
        ' Crible:
        For j = i * 2 To n Step i
            Nombre(j) = 1
        Next j
    End If
Next i
 
' Affichage dans une feuille Excel en colonne A (il ne manque que le 2):
y = 1
For i = 3 To n Step 2
    If Nombre(i) = 0 Then y = y + 1: Cells(y, "A") = i
Next i
 
End Sub

Le "problème" ici est que la taille de la mémoire est de n, alors que les colonnes pairs et les 5 ne sont pas utilisées.
J'ai donc cherché à faire un algorithme qui minimise la mémoire nécessaire, soit 4 colonnes au lieu de 10.
Le principe du crible consiste, à partir d'un nombre impair, de faire son décalage dans le tableau uniquement sur les colonnes 1, 3, 7, 9.
Je ne rentre pas dans le détail (car c'est un peu long à expliquer) sauf si vous m'en faite la demande.
Soit le code suivant (en Basic):

Code VB :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
 
Dim Nombre() As Byte
Dim Maxi as Long
 
'-------------------------------------------------------------------------------
Sub Eratosthene(n As Long)
'-------------------------------------------------------------------------------
' Retourne la liste des nombres premiers jusqu'à n.
'-------------------------------------------------------------------------------
Dim d As Long, y As Long
 
Maxi = n/10
 
' Variable qui va contenir les lignes des colonnes 1,3,7,9:
ReDim Nombre(1 To 4, 0 To Maxi) As Byte
 
' Traitement des 4 colonnes:
Eratosthene 1
Eratosthene 3
Eratosthene 7
Eratosthene 9
 
' Affichage dans une feuille Excel en colonne B (il ne manque que le 2, 3, 5, 7):
y = 4
For d = 1 To Maxi
    If Nombre(1, d) = 0 Then y = y + 1: Cells(y, "B") = d * 10 + 1
    If Nombre(2, d) = 0 Then y = y + 1: Cells(y, "B") = d * 10 + 3
    If Nombre(3, d) = 0 Then y = y + 1: Cells(y, "B") = d * 10 + 7
    If Nombre(4, d) = 0 Then y = y + 1: Cells(y, "B") = d * 10 + 9
Next d
 
End Sub
 
Private Sub Eratosthene(U As Byte)
Dim a As Byte, b As Byte, c As Byte
Dim Ma As Byte, Mb As Byte, Mc As Byte, Md As Byte
Dim d As Long, i As Long, j As Integer
 
' En cas de dépassement de mémoire, ignorer l'erreur
On Error Resume Next
 
' Configuration des déplacements pour chaque colonnes:
Select Case U
    Case 1: a = 0: b = 0: c = 0: Ma = 2: Mb = 3: Mc = 4: Md = 1: j = 1
    Case 3: a = 0: b = 2: c = 0: Ma = 4: Mb = 1: Mc = 3: Md = 2: j = 0
    Case 7: a = 2: b = 2: c = 2: Ma = 1: Mb = 4: Mc = 2: Md = 3: j = 0
    Case 9: a = 2: b = 4: c = 2: Ma = 3: Mb = 2: Mc = 1: Md = 4: j = 0
End Select
 
' Crible:
For i = j To Sqr(Maxi)
    d = i
    Do
        d = d + i * 2 + a
        Nombre(Ma, d) = 1 ' 1ere colonne
        d = d + i * 4 + b
        Nombre(Mb, d) = 1 ' 2ème colonne
        d = d + i * 2 + c
        Nombre(Mc, d) = 1 ' 3ème colonne
        d = d + i * 2 + 1
        Nombre(Md, d) = 1 ' 4ème colonne
    Loop While d < Maxi
Next i
 
End Sub

Au final : réduction de 60% de la mémoire utilisée, réduction de 20% du temps de traitement.

D'où mes questions :
est-ce qu'il existe des améliorations au crible d’Ératosthène ?
est-ce qu'il existe un algorithme plus rapide ?

Sachant que cela n'a aucun intérêt en pratique, c'est juste pour ma culture générale.
Cordialement.

[tbc92]

Ici, dans ta réflexion, tu est 'déformé' par le fait qu'on écrive traditionnellement en base 10. Et du coup, tu privilégies les 2 nombres premiers 2 et 5.
Tu parles de tableau à 10 colonnes : le chiffre des unités en écriture en base 10.
Tu peux décliner l'idée avec un tableau à 6 colonnes : en travaillant modulo 6, au lieu de modulo 10.

Chez toi, tu pars de la règle : les nombres premiers sont forcément de la forme 10k+1, 10k+3, 10k+7 ou 10k+9 (hormis les nombres premiers plus petits que 10). Cette règle devient : les nombres premiers sont forcément de la forme 6k+1 ou 6k+5 (hormis les nombres premiers plus petits que 6).
Là où tu économisais 60% d'espace, on économise maintenant 66.6%.

Et on peut aussi travailler modulo 30 (6=le produit des 2 plus petits nombres premiers, 30=le produit des 3 plus petits nombres premiers).
Et on a cette règle : les nombres premiers sont forcément de la forme 30k+a avec a=1,7,11,13,17,19,23 ou 29. Hormis les nombres premiers plus petits que 30.
Au lieu d'avoir un tableau avec 30 colonnes, il suffit de traiter 8 colonnes sur 30, soit une économie de 73.3%

Et bien entendu, en travaillant modulo 210, on va encore gagner un petit peu.

[laurent_ott]

Ici, dans ta réflexion, tu est 'déformé' par le fait qu'on écrive traditionnellement en base 10... Et on peut aussi travailler modulo 30 (6=le produit des 2 plus petits nombres premiers, 30=le produit des 3 plus petits nombres premiers).
Et on a cette règle : les nombres premiers sont forcément de la forme 30k+a avec a=1,7,11,13,17,19,23 ou 29. Hormis les nombres premiers plus petits que 30.
Au lieu d'avoir un tableau avec 30 colonnes, il suffit de traiter 8 colonnes sur 30, soit une économie de 73.3%
Et bien entendu, en travaillant modulo 210, on va encore gagner un petit peu.

Bonjour.
J'ai généré un tableau des nombres premiers en base 30 pour mieux comprendre le principe:



Et j'avoue avoir pas mal galéré pour programmer le crible.
Je ne rentre pas dans le détail (car c'est un peu long à expliquer) sauf si vous m'en faite la demande.
Au final il y a environ 4 fois moins de mémoire utilisée (comme l'a expliqué "tbc92"), et le temps de traitement est lui aussi divisé par 4 environ (sur mon PC et en VBA).
Soit le code suivant (en Basic):

Code VB :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
 
Dim Nombre() As Byte
Dim Maxi As Long
 
'---------------------------------------------------------------------------------------
Sub NombresPremiersJusqua(n As Long)
'---------------------------------------------------------------------------------------
Dim d As Long, y As Long
 
' Dimensionnement de la mémoire qui contiendra les nombres analysés:
Maxi = n / 30
ReDim Nombre(1 To 8, 0 To Maxi) As Byte
 
' Traitement du crible Eratosthene en base 30 sur les colonnes:
Eratosthene_30 1, n
Eratosthene_30 7, n
Eratosthene_30 11, n
Eratosthene_30 13, n
Eratosthene_30 17, n
Eratosthene_30 19, n
Eratosthene_30 23, n
Eratosthene_30 29, n
 
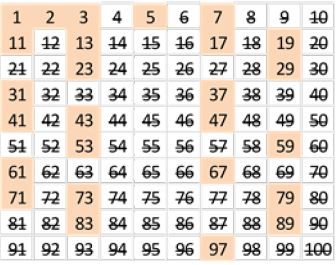
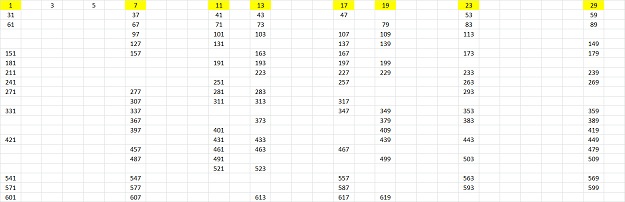
' Affichage sur une feuille Excel (manque les premiers 1,3,5,7,11,13,17,19,23,29):
y = 10
For d = 1 To Maxi
    If Nombre(1, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 1
    If Nombre(2, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 7
    If Nombre(3, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 11
    If Nombre(4, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 13
    If Nombre(5, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 17
    If Nombre(6, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 19
    If Nombre(7, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 23
    If Nombre(8, d) = 0 Then y = y + 1: Cells(y, "B") = d * 30 + 29
Next d
 
End Sub
 
'---------------------------------------------------------------------------------------
Private Sub Eratosthene_30(U As Byte, n As Long)
'---------------------------------------------------------------------------------------
Dim a As Byte, b As Byte, c As Byte, d As Byte, e As Byte, f As Byte, g As Byte, h As Byte
Dim i As Long, j As Integer, m As Byte
Dim z As Variant, y As Long
z = CDec(z)
 
' Mémoires pour le décalage des lignes:
Dim Décal(0 To 7) As Long
Dim base
base = Array(6, 10, 12, 16, 18, 22, 28, 30)
 
' Ne pas tenir compte du débordement dans le mémoire Nombre():
On Error Resume Next
 
' Initilialisation des colonnes concernées:
Select Case U
    Case 1: a = 2: b = 3: c = 4: d = 5: e = 6: f = 7: g = 8: h = 1: j = 1
    Case 7: a = 6: b = 5: c = 1: d = 8: e = 4: f = 3: g = 7: h = 2: j = 0
    Case 11: a = 5: b = 1: c = 7: d = 2: e = 8: f = 4: g = 6: h = 3: j = 0
    Case 13: a = 1: b = 7: c = 6: d = 3: e = 2: f = 8: g = 5: h = 4: j = 0
    Case 17: a = 8: b = 2: c = 3: d = 6: e = 7: f = 1: g = 4: h = 5: j = 0
    Case 19: a = 4: b = 8: c = 2: d = 7: e = 1: f = 5: g = 3: h = 6: j = 0
    Case 23: a = 3: b = 4: c = 8: d = 1: e = 5: f = 6: g = 2: h = 7: j = 0
    Case 29: a = 7: b = 6: c = 5: d = 4: e = 3: f = 2: g = 1: h = 8: j = 0
End Select
 
' Calcul du décalage pour l'unité passée en argument:
z = j * 30 + U
Décal(0) = Int((z * 7) / 30) - j
Décal(1) = Int((z * 11) / 30) - j
Décal(2) = Int((z * 13) / 30) - j
Décal(3) = Int((z * 17) / 30) - j
Décal(4) = Int((z * 19) / 30) - j
Décal(5) = Int((z * 23) / 30) - j
Décal(6) = Int((z * 29) / 30) - j
Décal(7) = z
 
' Boucle sur les nombres de l'unitée:
For i = j To (Sqr(n) / 30) + 1
 
    ' Crible:
    y = i
    Do
        Nombre(a, y + Décal(0)) = 1
        Nombre(b, y + Décal(1)) = 1
        Nombre(c, y + Décal(2)) = 1
        Nombre(d, y + Décal(3)) = 1
        Nombre(e, y + Décal(4)) = 1
        Nombre(f, y + Décal(5)) = 1
        Nombre(g, y + Décal(6)) = 1
        Nombre(h, y + Décal(7)) = 1
        y = y + Décal(7)
    Loop While y < Maxi
 
    ' Nouveau décalage:
    For m = 0 To 7
        Décal(m) = Décal(m) + base(m)
    Next m
 
Next i
 
End Sub
'---------------------------------------------------------------------------------------
'---------------------------------------------------------------------------------------

Merci pour cette méthode.
Je n'ai pas essayé en base 210.

[tbc92]

Le tableau avec les 30 colonnes montre très bien que les nombres premiers sont concentrés sur 8 colonnes. La démonstration 'mathématique' serait assez simple.
Il manque juste le nombre 2 comme nombre premier