Si j'ai bien compris, l'utilisateur 1 dans le tableau est « l'utilisateur qui effectue la requête ».
Il ne devrait donc pas figurer dans le tableau, mais plutôt en dehors, comme référence.
Je vais donc partir sur cette base-là, en notant :
- p1, …, pn les produits que l'utilisateur de référence a choisi en position 1, …, position n ;
- u l'indice de l'utilisateur dans le tableau ;
- I(u,pi) =
| (la place à laquelle se trouve le produit pi pour l'utilisateur u) - i |, si l'utilisateur u a choisi ce produit ;
n, sinon ;
- C1(u,pi) =
1, si l'utilisateur u n'a pas choisi le produit pi, et sinon :
(n - 1) / (n - i), pour 1 ≤ i ≤ n/2 si n est pair, pour 1 ≤ i ≤ (n+1)/2 si n est impair ;
(n - 1) / (i - 1), pour n/2+1 ≤ i ≤ n si n est pair, pour (n+1)/2 ≤ i ≤ n si n est impair ;
- C2(pi) = (n - i + 1) / n.
Ainsi, on va pouvoir affecter à tout utilisateur u une distance le séparant de l'utilisateur de référence : D(u) = C1(u,p1)C2(p1)I(u,p1) + … + C1(u,pn)C2(pn)I(u,pn).
On peut vérifier que si u est l'utilisateur de référence, D(u) = 0, car par définition, I(u,pi) = 0 pour tout i.
Les C1(u,pi) sont là pour corriger la pondération implicite (et injustifiée) qu'introduit la définition des I(u,pi) : moins d'importance aux produits choisis vers le milieu (i proche de n/2).
Les C2(pi) sont une manière de pondérer la somme pour que les choix des utilisateurs soient d'importance décroissante du produit 1 au produit n : on peut en imaginer plein d'autres.
+++
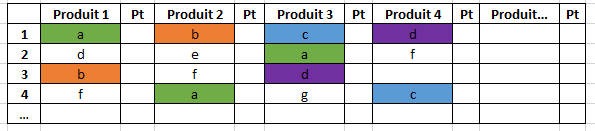
Appliqué à l'exemple, voilà ce que ça donne :
D(2) = 1*1*2 + 1*3/4*4 + 1*2/4*4 + 1*1/4*4 = 8
D(3) = 1*1*4 + 3/2*3/4*1 + 1*2/4*4 + 1*1/4*1 = 59/8 = 7,375
D(4) = 1*1*1 + 1*3/4*4 + 3/2*2/4*1 + 1*1/4*1 = 23/4 = 5,75
On obtient donc un résultat où l'utilisateur 2 est plus éloigné de la référence que l'utilisateur 3 : il faut dire que l'utilisateur 3 coche 2 cases, quand l'utilisateur 2 n'en coche qu'une, et que les cases que l'utilisateur 3 coche sont moins éloignées de la référence que celle que coche l'utilisateur 2.
Ça n'est donc pas absurde, mais si on veut que le produit 1 ait un poids relatif plus important dans le calcul de la distance, de sorte que l'utilisateur 2 apparaisse finalement moins éloigné de la référence que l'utilisateur 3, on peut jouer sur la pondération C2(pi), en l'élevant par exemple au carré :
C2(pi) = (n - i + 1)2 / n2
Avec cette nouvelle pondération, on obtient :
D(2) = 1*1*2 + 1*9/16*4 + 1*4/16*4 + 1*1/16*4 = 11/2 = 5,5
D(3) = 1*1*4 + 3/2*9/16*1 + 1*4/16*4 + 1*1/16*1 = 5 + 29/32 = 5,90625
D(4) = 1*1*1 + 1*9/16*4 + 3/2*4/16*1 + 1*1/16*4 = 31/8 = 3,875
Cette fois-ci, l'utilisateur 3 est donc plus éloigné de la référence que l'utilisateur 2.
Algorithme de correspondance par point
Répondre avec citation
en bas à droite du message.
Partager