je voudrais vérifier si la complexité du bout de code suivant est nlogn ?
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
 Discussion :
Discussion :
je voudrais vérifier si la complexité du bout de code suivant est nlogn ?
Code : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
La question est plus ou moins : combien de fois on passe par la ligne n°6 de ce programme.
Si n est grand (disons 10 Millions), on va passer par cette ligne combien de fois ?
+20 Millions de fois quand i vaut 10 Millions
+10 Millions de fois quand i vaut 5 Millions
+5 Millions de fois quand i vaut 2.5 Millions
Etc. En tout, on passe 40 Millions de fois par cette ligne n°6.
Et quand n vaut 10 Milliards, On va multiplier tous ces nombres par 1000... donc non, la complexité n'est pas en n*log(n).
N'oubliez pas le bouton Résolu si vous avez obtenu une réponse à votre question.
Quelques questions pour t'aider à trouver la réponse :
- combien de fois la boucle intérieure (sur j) est-elle exécutée, en fonction de i et de n ?
- combien de fois la boucle extérieure (sur i) est-elle exécutée, uniquement en fonction de i ?
- combien vaut la somme ?
Ma solution :
Vous souhaitez participer aux rubriques Qt (tutoriels, FAQ, traductions) ou HPC ? Contactez-moi par MP.
Créer des applications graphiques en Python avec PyQt5
Créer des applications avec Qt 5.
Pas de question d'ordre technique par MP !
la boucle a l’intérieur est exécutée 2n(1+1/2+1/2^2+1/2^3+1/2^4+...........+1/2^logn)
donc a quoi est égale cette somme ?
la boucle a l’intérieur est exécutée 2n(1+1/2+1/2^2+1/2^3+1/2^4+...........+1/2^logn) : oui
a quoi est égale cette somme ? : relis la discussion. Sachant qu'on a simplement besoin d'une estimation plus ou moins précise.
N'oubliez pas le bouton Résolu si vous avez obtenu une réponse à votre question.
donc la complexité sera inférieure a n*log n et je crois qu'elle doit être aussi supérieure a log^2n ?
quelle est la solution ?
je crois que ça sera log(logn)*n
N+ N/2 + N/4 + N/8 ... etc , ça vaut 2N
Ici, la somme commence par 2N + N + N/2 +N/4 ... donc ça donne 4N.
Si on veut être pécis, ça donne 4N-1 ; mais pour un calcul de complexité, c'est 4N. Surtout qu'il y a un autre petit truc qui fait des différences, c'est qu'on divise par 2 à chaque étape, et on arrondit à l'entier inférieur si la division par 2 ne tombe pas juste. Et notre calcul ne tient pas compte de cet arrondi.
A mon avis, pas de log() dans le résultat, même si effectivement, dans les étapes intermédiaires, il y a du log().
N'oubliez pas le bouton Résolu si vous avez obtenu une réponse à votre question.
N'y a-t-il pasitérations en tout ? Ce qui est égal à
si on ne prend pas la partie entière, ce qui correspond à une complexité de
.
Par exemple, si on part avec n=16, la boucle principale itérera 5 fois:
- i=16 -> j=32 -> +31 itérations
- i=8 -> j=16 -> +15 itérations
- i=4 -> j=8 -> +7 itérations
- i=2 -> j=4 -> +3 itérations
- i=1 -> j=2 -> +1 itération
Au total, il y a 31+15+7+3+1=57 itérations.
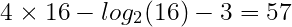
Vous avez un bloqueur de publicités installé.
Le Club Developpez.com n'affiche que des publicités IT, discrètes et non intrusives.
Afin que nous puissions continuer à vous fournir gratuitement du contenu de qualité, merci de nous soutenir en désactivant votre bloqueur de publicités sur Developpez.com.
Partager