Jetbrains annonce la disponibilité d'Arend 1.0.0, son assistant de preuve,
qui est basé sur la théorie des types d'homotopie
Arend est un assistant de preuve basé sur la théorie des types d'homotopie. En informatique (ou en mathématiques assistées par informatique), un assistant de preuve est un logiciel permettant l'écriture et la vérification de preuves mathématiques, soit sur des théorèmes au sens usuel des mathématiques, soit sur des assertions relatives à l'exécution de programmes informatiques. Arend supporte nativement les types inductifs supérieurs et une version de la syntaxe cubique. IntelliJ Arend est un plugin pour IntelliJ IDEA qui le transforme en un IDE à part entière pour le langage Arend.
Arend implémente une version de la théorie des types d'homotopie avec un type d'intervalle, dont la syntaxe est similaire à la théorie des types cubiques. Cela implique plusieurs propriétés intéressantes des types de chemins et permet une définition simple et nette des types inductifs supérieurs (y compris les types récursifs).
Arend dispose d'un système de classes puissant, qui prend en charge l'inférence d'instance de style Haskell. L'héritage de classe peut être utilisé pour définir diverses hiérarchies de structures (algébriques). Arend a également un mécanisme simple et puissant pour gérer les niveaux de l'univers.
Caractéristiques d'homotopie
Arend est basé sur la théorie des types d'homotopie avec un type d'intervalle. Cela signifie qu'il a un type d'intervalle contractile intégré ainsi que deux constructeurs left, right : I. Nous pouvons utiliser ce type pour définir le type de cubes à n dimensions comme \Sigma I … I, c'est-à-dire comme le produit de n intervalles. Ces types ne sont pas très intéressants en eux-mêmes, car ils sont contractiles, mais ils peuvent être utilisés comme types de cellules dans la définition d'un type inductif d'ordre supérieur.
Types de chemin
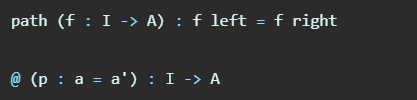
Un chemin dans un type A entre les points a, a ': A est une fonction f: I -> A telle que f left == a et f right == a' (nous utilisons “==” pour désigner l'égalité de définition). Le type de chemins est noté a = a ’. Pour obtenir un chemin d'une fonction et vice versa, nous pouvons utiliser les fonctions suivantes:
La fonction @ est généralement écrite sous la forme d'un infixe et se prononce «at». Le chemin de la fonction est en réalité le seul constructeur du type de données =. Les fonctions path et @ sont inverses, c'est-à-dire path f @ i == f i et path (\lam i => p @ i) == p.
Cette définition des types de chemin a plusieurs propriétés intéressantes. Premièrement, toutes les constructions habituelles (telles que la concaténation de chemins, le transport et la règle J) peuvent être définies pour elles. De plus, certaines de ces constructions satisfont des égalités de calcul supplémentaires. Par exemple, nous pouvons définir la fonction qui applique une carte à un chemin comme suit :
Cette fonctionnalité est strictement fonctionnelle, raison pour laquelle nous avons les égalités pmap id p == p et pmap (\lam x => g (f x)) p == pmap g (pmap f p).
Il est également plus facile de prouver une extensionnalité fonctionnelle :
Cette fonction satisfait également diverses égalités de définition, ce qui signifie que nous pouvons facilement passer entre l’égalité des fonctions et leur égalité ponctuelle.
Types inductifs d'ordre supérieur
Un type inductif d'ordre supérieur est un type de données dont les constructeurs sont des cellules supérieures. Par exemple, la sphère à une dimension peut être définie comme le type de données avec une base de point et un constructeur loop à une dimension attaché à ce point:
Les constructeurs supérieurs tels que loop fonctionnent comme des fonctions ordinaires: loop leftet loop right sont évaluées à la base. La syntaxe de ces constructeurs est la même que celle des fonctions définies par correspondance.
Nous pouvons également attacher des cellules de dimensions encore plus élevées. Par exemple, la sphère à deux dimensions peut être définie comme le type de données avec un point base2 et un constructeur à deux dimensions loop2 attaché à ce point. Comme la limite d'un cube à 2 dimensions est constituée de quatre cubes à une dimension, nous devons spécifier quatre conditions sur le constructeur loop2:
Les fonctions sur des types inductifs d'ordre supérieur peuvent être définies par correspondance, comme d'habitude. La seule différence est qu'il est nécessaire qu'ils respectent les équations sur les constructeurs. Par exemple, pour définir une fonction S2 -> T, nous devons spécifier un point b : T et une fonction l : I -> I -> T tel que l left _ == b, l right _ == b, l _ left == b et l _ left == b:
Si cette définition ne remplit pas les conditions décrites ci-dessus, un message d'erreur sera généré.
Types de données tronqués
Les types de données tronqués peuvent être définis comme des types inductifs d'ordre supérieur, mais il existe un moyen plus simple de le faire. Un type de données peut être défini comme [C]\ truncated[/X], ce qui signifie qu'il sera tronqué au niveau d'homotopie spécifié. Par exemple, les quotients peuvent être définis comme suit:
Ces types de données ne peuvent être éliminés que dans les types du niveau d'homotopie correspondant.
Pattern Matching
Une correspondance de modèle sur un type inductif d'ordre supérieur peut être simplifiée si l'objectif a un niveau d'homotopie fini. Pour définir une fonction dans un type n, il suffit de spécifier ses valeurs pour les constructeurs de dimension inférieure ou égale à n + 1. Par exemple, si X est un ensemble, pour définir une fonction Quotient AR -> X, il est suffisant de spécifier sa valeur pour chaque a: A et prouver que cette définition respecte la relation d'équivalence (cette preuve est la valeur correspondant au second constructeur). Cela fonctionne pour la définition des quotients que nous avons donnée ci-dessus et aussi pour les quotients définis comme un type inductif d'ordre supérieur.
Si P x est une proposition, pour définir une fonction \ Pi (x: quotient AR) -> P x, il suffit de le spécifier pour le constructeur in~. Cela devient encore plus utile lorsque P dépend de plusieurs éléments du quotient. Par exemple, si nous avons 3 éléments x, y, z: Quotient AR (qui est défini comme un type inductif d'ordre supérieur à 3 constructeurs), il suffit alors de prouver une propriété à leur sujet au lieu de neuf.
Système de classe
Arend a des enregistrements et des classes. Les classes ne sont que des enregistrements avec des fonctionnalités supplémentaires, ce qui les transforme en classes de type haskell.
Héritage
Les enregistrements ne sont que des types Sigma avec des champs nommés. Par exemple, nous pouvons définir le type de monoids comme suit :
Les enregistrements peuvent être hérités. Si un enregistrement étend un enregistrement de base, il aura les mêmes champs que celui de base avec ses propres champs. Par exemple, nous pouvons définir un groupe en tant que monoïde avec trois champs supplémentaires :
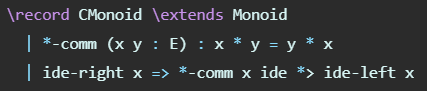
Les extensions peuvent également implémenter certains des champs de l'enregistrement de base. Un tel enregistrement est équivalent au type Sigma qui contient tous les champs non implémentés. Par exemple, le type de monoïde commutatif peut être défini comme suit:
Pour les monoïdes commutatifs, il suffit de prouver que ide est l’identité de gauche puisque le fait qu’elle est la bonne identité découle de la commutativité. Nous pouvons le prouver dans la définition des monoïdes commutatifs en implémentant le champ correspondant.
Les enregistrements prennent également en charge l'héritage multiple. Par exemple, nous pouvons définir le type de groupes commutatifs simplement en étendant les types de groupes et de monoïdes commutatifs:
Extensions anonymes
Les paramètres des enregistrements sont en réalité leurs champs. Ainsi, les deux définitions suivantes des ensembles pointus sont en réalité équivalentes:
La raison pour laquelle Arend n’a pas de paramètres d’enregistrement, c’est parce qu’il a plutôt des extensions anonymes. Une extension anonyme d'un enregistrement R est une expression de la forme R { | f_1 => e_1 … | f_n => e_n }, où f_1, … f_n sont des champs de R et e_1, … e_n sont des expressions des types correspondants. Une telle expression est identique à un enregistrement qui étend R et implémente des champs spécifiés, mais il n’est pas nécessaire de définir cet enregistrement séparément. L'extension anonyme décrite ci-dessus peut également être écrite sous la forme R e_1… e_n. Dans ce cas, les champs sont implémentés dans le même ordre que celui défini dans l'enregistrement.
Considérons quelques exemples:
- Le type Monoid est le type de monoïde.
- Le type Monoid Nat est le type de structure monoïde de l'ensemble Nat.
- Le type Monoid Nat 1 (Nat. *) est le type de preuves que 1 et Nat. * déterminent la structure d'un monoïde sur Nat.
Notez que les deux derniers exemples donnent l'impression que le type de monoïde a été défini avec 1 et 3 paramètres, respectivement. Ainsi, nous n'avons pas à nous demander quels champs doivent être définis en tant que paramètres et lesquels doivent être laissés en tant que champs. Nous pouvons utiliser n’importe quel enregistrement comme s’il était défini en même temps dans tous ces styles.
Classes
Disons que nous avons la définition des monoïdes telle que décrite ci-dessus. Ensuite, nous voulons écrire des expressions de la forme (x * y) * ide * z, mais nous ne pouvons pas le faire. La raison en est que * et ide sont des champs. Cela signifie qu'ils nécessitent un argument supplémentaire, une instance de Monoid. Les instances d'enregistrements ne peuvent généralement pas être déduites automatiquement. Pour cette raison, il est préférable de définir Monoid en tant que classe. Une classe est définie de la même manière qu’un enregistrement, mais avec le mot-clé \ class au lieu de \ record.
Les instances de classes sont déduites automatiquement. Cet algorithme d'inférence recherche des instances à deux endroits. Tout d'abord, il recherche les paramètres d'une définition dans laquelle se trouve l'appel de champ. S'il existe un paramètre approprié, il sera utilisé comme instance de classe. Par exemple, les instances de la fonction test ci-dessous seront déduites comme indiqué dans test2.
Code Arend : Sélectionner tout - Visualiser dans une fenêtre à part
2\func test {M : Monoid} (x y z : M) => (x * y) * ide * z \func test2 {M : Monoid} (x y z : M) => (x M.* y) M.* M.ide M.* z
S'il n'y a pas d'instance locale appropriée, l'algorithme recherchera l'ensemble des instances globales. Une instance globale est simplement une fonction définie en utilisant le mot-clé \ instance au lieu de \ func. Par exemple, nous pouvons prouver que Nat est une instance de la classe Monoid et utiliser cette instance comme indiqué ci-dessous:
Code Arend : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8\instance NatMonoid : Monoid Nat | ide => 1 | * => Nat.* | ide-left x => {?} -- the proofs are omitted | ide-right x => {?} | *-assoc x y z => {?} \func test (x y z : Nat) => (x * y) * 1 * (z * ide)
Niveaux d'Univers
Arend a une hiérarchie d'univers paramétrés par deux nombres naturels. Le premier paramètre correspond au niveau habituel (prédicatif) de l'univers. Le deuxième paramètre correspond au niveau d'homotopie des types dans cet univers. L'univers de niveau (p, h) est écrit comme \ h-Type p. L’univers \ 0-Type p peut être abrégé en \ Set p. Nous pouvons aussi écrire \ Type p h au lieu de \ h-Type p.
Les niveaux ne peuvent pas être ajoutés les uns aux autres, mais nous avons la fonction successeur \ suc et la fonction maximale \ max. Il existe également le plus grand niveau d’homotopie \ oo, qui correspond aux types non tronqués.
L'univers \ h-Type p appartient à l'univers \ (h + 1) -Type (p + 1). Les univers sont cumulatifs: si A: \ h-Type p, alors A: \ h’Type p' pour tous les h’ et p' supérieurs ou égaux à h et p, respectivement.
Téléchargez Arend
Source : Arend

















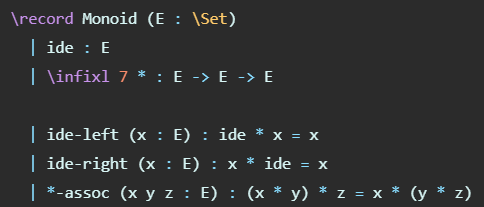



 Répondre avec citation
Répondre avec citation
Partager