Discussion :

[bebdoo]

Bonjour à tous
Dans le but d'optimiser le parcours d'une machine à commande numerique
voila une photo de l'application sur bois : (là c'est un essai en petit)

je cherche un algo qui permet de joindre tous les polygones cote à cote (si possible). (ensuite je trouverais un autre algo qui permettra de creer qu'une seule ligne)
ca peut etre en spirale en partant de l'exterieur ou en ligne de haut en bas, de gauche à droite puis droite à gauche etc (j'ai une fonction qui permet de calculer le centre de chaque polygone)


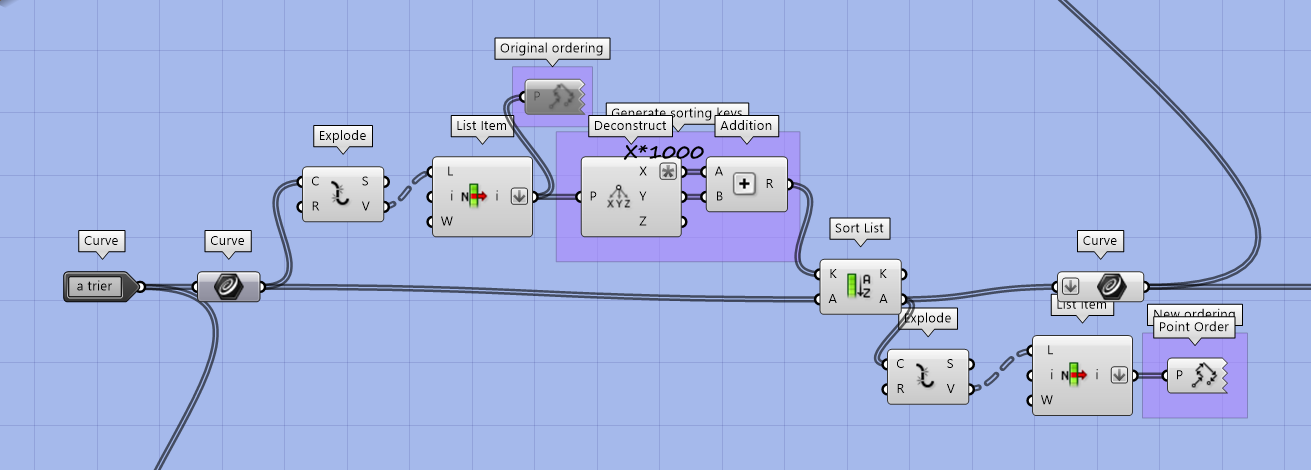
En fait , j'ai fait un premier algo pour essayer de faire qu'une seule ligne:
Je decomposais tous les polygones puis j'effacais les doublons (lignes et points)
Apres je cherche les points de degré impairs
j'applique l'algo de dijskstra pour creer des lignes supplementaires pour joindre les impairs 2 par 2 par leur chemin le + court pour n'avoir que des points de degré pairs et ainsi pouvoir appliquer l'algo de d'euler (mais il ne fallait pas quil y ait 3 segments qui se superposent ...)
ensuite je fais l'algo d'euler pour joindre toutes les lignes en une seule (qui fonctionne que si tous les points sont de degré pairs)
le problème c'est qu'il y avait toujours des cas particuliers , c'etait beaucoup trop compliqué , j'y ai passé trop de temps pour que ca ne marche pas. C'est un peu comme qd on attend le bus, a partir de quel moment on s'en va ou non ...

Avez vous des idées ?

Pierre

[wiwaxia]

Bonjour,

Tu as à priori fait l'inventaire des polygones, de leurs arêtes et de leurs sommets, ainsi que de leur centre C_k(x_k, y_k) - barycentre des sommets sans doute ? mais passons. C'est un bon départ.

... je cherche un algo qui permet de joindre tous les polygones côte à côte (si possible). (ensuite je trouverais un autre algo qui permettra de créer qu'une seule ligne)
Ça peut être en spirale en partant de l'extérieur ou en ligne de haut en bas, de gauche à droite puis droite à gauche etc (j'ai une fonction qui permet de calculer le centre de chaque polygone) ...

C'est là qu'on aborde le fond du problème: l'inventaire systématique des polygones suppose la définition d'une relation d'ordre entre eux (ou leurs centres, ce qui revient au même), définition intrinsèquement liée au mode de parcours du domaine considéré:
Par exemple (C_i) a préséance sur (C_j) si et seulement si:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
 
// Critère (1): balayage vertical
 Test1:= ((X[i]<X[j]) OR ((X[i]=X[j]) AND (Y[i]<Y[j])));
 
// Critère (2): balayage horizontal
 Test2:= ((Y[i]<Y[j]) OR ((Y[i]=Y[j]) AND (X[i]<X[j])));
 
// Critère (3): balayage en diagonale
 Test3:= ((X[i]+Y[i]<X[j]+Y[j]) OR ((X[i]+Y[i]=X[j]+Y[j])  AND (Y[i]<Y[j])));

mais le parcours n'aura de sens qu'après installation d'un super-quadrillage comportant (N_x) colonnes et (N_y) lignes, calculées à partir des dimensions du domaine, et du nombre (N_p) de polygones présents:
N_x = Round(L_arg / Sqrt(N_p)) ; N_y = Round((H_aut / Sqrt(N_p)) .
La définition de coordonnées secondaires relatives à la case du damier ainsi défini, et dans laquelle se trouve (C[k])
U[k] = Trunc(X[k]) / N_x) , V[k] = Trunc(Y[k]) / N_y)
permet d'envisager un parcours moins chaotique, en raison d'une réduction drastique des choix possibles:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
 
// Critère (1): balayage vertical de haut en bas
 
Test1:= ((U[i]<U[j]) OR ((U[i]=U[j]) AND ((V[i]<V[j]) OR ((V[i]=V[j]) AND (Y[i]<Y[j]))))) ;
 
// Critère (2): balayage horizontal de gauche à droite
 
Test2:= ((V[i]<V[j]) OR ((V[i]=V[j]) AND ((U[i]<U[j]) OR ((U[i]=U[j]) AND (X[i]<X[j]))))) ;

Un parcours alternatif , comportant des zigzags, apparaîtra encore plus difficile à coder. Pour une progression spiralaire effectuée à partir du centre, impliquant une comparaison des couples (r_k, t_k), il faudra constamment ré-évaluer les (N_p - k) angles polaires restant, qui ne sont définis qu'à (2*Pi) près; cependant l'obstacle n'est pas rédhibitoire.

Il faut considérer le graphe dual associé à la partition du domaine, dont les sommets sont les centres des polygones ⁽¹⁾, et admettant pour arêtes l'ensemble (E_A) des arcs vérifiant:
(C_iC_j) appartient à (E_A) si et seulement si (Pol_i) adjacent à (Pol_j) .
Tu cherches en fait un parcours hamiltonien, et il n'est pas évident qu'un tel parcours existe, les limites du domaine constituant une contrainte importante.

... je cherche un algo qui permet de joindre tous les polygones côte à côte (si possible) ...

Un parcours en spirale amorcé sur le polygone le plus central, et recherchant en priorité les domaines adjacents les plus proches, constituera une solution acceptable ... mais il ne faudra guère compter sur une suite ininterrompue de polygones adjacents.
On peut aussi envisager une présélection grossière des centres, utilisant le quadrillage précédemment décrit.

⁽¹⁾ Plus les quatre coins du domaine ...

[tbc92]

Ce que tu cherches à faire, c'est :
- relier tous les polygones par une ligne, en passant une fois et une seule par chaque polygone, point final.
- relier tous les polygones par une ligne, en passant une fois et une seule par chaque polygone, et en appliquant un thème ( spirale, zig-zag .... )

[pseudocode]

je cherche un algo qui permet de joindre tous les polygones cote à cote (si possible).

Ce n'est pas toujours possible.

+--+---+--+
|  |   |  |
+--+   +--+
|         |
+---------+
|         |
+---------+

Ceci étant posé, comme le dis wiwaxia, il te faut une règle pour définir un ordre.

Par exemple, se déplacer vers le prochain polygone non traversé qui a son centre le plus près du bord (parcours en spirale).

[bebdoo]

Merci pour vos réponses
Pseudocode, je pense que je n'aurais jamais ce cas de figure car j'aurais toujours un grand nombre de polygones et ce ne sera pas possible qu'un polygone touche à la fois l'arete gauche et droite du rectangle englobant

Par exemple, se déplacer vers le prochain polygone non traversé qui a son centre le plus près du bord (parcours en spirale).

c'est une très bonne idée, il faut que je regarde comment je peux coder ca, cet algo ce serait l'idéal, (en zigzag serait bien aussi )


Pour le moment j'arrive juste à faire un tri d'abord des Y puis des X, ce n'est pas terrible
voila l'algorithme, en gros: j'explose tous les polygones, je récupere chaque point (Vertices), j'additionne leur (X*1000) + Y pour chaque point, et je fais un tri des polygones avec cette valeur:


Ca me donne ca :



Je vais laisser tomber le parcours hamiltonien s'il y a trop de cas particuliers

[anapurna]

salut

il y a pas de cas particulier
en prenant les centres des polygones et les arrêtes commune à deux polygones tu devrais t'en sortir sans soucis
il faut juste vérifier que le lien entre deux polygone n'as pas déjà été créé
donc on résume
1°) tu fais la liste de tout les polygone(liste des points et des droite constituant ton polygone)
2°) tu calcul pour chaque polygone le centre et tu recenses tous ces voisins
3°)pour chaque polygone tu prend le centre et tu le relis au centre de son voisin en vérifiant que tu n'as pas déjà créé le liens
normalement une fois fait ça tu as obtenu ton graphe

[wiwaxia]

Il me vient une idée idiote, mais qui répond littéralement à l'énoncé de ton projet:

... je cherche un algo qui permet de joindre tous les polygones côte à côte (si possible). (ensuite je trouverais un autre algo qui permettra de créer qu'une seule ligne) ...

appliquer à l'ensemble des centres (C_k) l'algorithme du voyageur de commerce, qui te permettra de relier les points les plus proches, à défaut de correspondre à des polygones adjacents; tu ne perds rien sur ce point, le graphe dual n'étant probablement pas hamiltonien.

Si l'idée d'une chaîne fermée te gêne, tu peux t'orienter vers la recherche du plus court trajet entre deux points extrêmes, qui n'est qu'une variante du problème précédent.
Les points en cause seraient donnés par les valeurs extrêmes de la somme (S_k = x_k + y_k): minimum (coin supérieur gauche) et maximum (coin inférieur droit).

Cela implique bien sûr de renoncer au type de parcours dont tu rêvais, en zigzags quasi-parallèles à l'un des bords ou l'une des diagonales; cependant cette idée séduisante me paraît tout aussi illusoire que la précédente, ou tout au moins très difficile à réaliser ... Y renoncer t'épargnerait sans doute beaucoup d'ennuis - à moins évidemment qu'un autre intervenant ne propose une solution inattendue.