Exercice corrigé d’algorithmique (Force 5/7)
Public :
- étudiants
- débutants
- et pourquoi pas, enseignants
Contenu :
- Logique séquentielle
- Simulation (Excel)
- Algorithme
- Algorigramme
TUTORIEL
Homogénéiser la répartition d'un tableau
■ ■ ■ SOMMAIRE DU BILLET ■ ■ ■
- Homogénéiser la répartition d’un tableau
- La problématique
- La pédagogie « Inspecteur Colombo »
- Simulation
- Tableaux Excel
- Les données et leur calcul
- Homogénéisation des pourcentages
- Calcul des intervalles 50% jetons verts
- Calcul des intervalles 30% jetons rouges
- Calcul des intervalles 10% jetons bleus
- Calcul des intervalles 7% jetons jaunes
- Calcul des intervalles 3% jetons noirs
- Homogénéisation de la Playlist via une matrice (100 x 5)
- Algorigramme pour renseigner une matrice
- Algorigramme pour créer la Playlist depuis une matrice
- Homogénéisation de la Playlist via une BDD
- Algorigramme pour créer une table "couleur" BDD
- Algorigramme pour créer la Playlist depuis une table BDD
- Conclusion
■ AVANT-PROPOS
- Présentation du sujet
Comment répartir des jetons de couleurs différentes (50% vert, 30% rouge, 10% bleu, 7% jaune, 3% noir) dans un tableau de 100 cases, de la façon la plus homogène possible ?
Ce tutoriel d’algorithmique s’inspire d'une discussion initiée le 27/12/2022 par petit_chat sur le Forum Algorithmes et structures de données :
- Motivations et raisons ayant poussé à étudier le sujet
Sûrs de leur technicité et de leur logique combinatoire, les intervenants prétendent résoudre la problématique en quelques lignes de code Python.
Pas convaincu par leur raisonnement alambiqué, leur logique combinatoire indigeste et leurs explications confuses qui imaginent, supposent ou conditionnent, j’ai abordé cette problématique autrement, comme un défi à ma logique, pour concevoir non pas un mais deux algorithmes fiables à 100%.
Les règles et techniques algorithmiques diffèrent selon le type de problématique. La logique adoptée peut être combinatoire ou séquentielle :
- La logique combinatoire raisonne selon la règle des trois unités : unité d’action, unité de temps et unité de lieu.
L’algorithmique formalise ce raisonnement dont les résultats sont fonction et seulement fonction des données traitées dans l'instant.
- La logique séquentielle imagine plusieurs actions s’exécutant successivement, chaque action étant traitée en logique combinatoire. Pour chaque action, les résultats ne dépendent pas seulement des données traitées dans l'instant mais aussi des données traitées précédemment.
L’Algorithmique séquentielle ou logique séquentielle correspond à la conception d’une succession d’étapes appelées sous-états dont chacun est en interaction avec les sous-états qui le précèdent.
Sans formalisme particulier, l’algorithmique séquentielle conçoit, construit cette interdépendance entre les sous-états.
En d’autres termes, il s’agit d’être créatif face à la spécificité de la problématique.
- Objectif poursuivi :
Réaliser un tutoriel pour partager une approche de la problématique faisant appel à une logique séquentielle. La démarche est bien loin de la logique combinatoire adoptée par les intervenants dans la discussion.
Originale, la pédagogie adoptée propose d’emblée la solution avant d’expliquer la démarche ayant conduit à cette solution.
Documentspubliés : le présent Billet de blog et ce tutoriel au format PDF :
- Difficultés rencontrées
Une difficulté a été de réaliser manuellement, calculette en main, l’affectation homogène des jetons, couleur par couleur, dans un tableau des pourcentages.
Ce tableau terminé, la conception de la Playlist qui n’était pas préméditée, s’est imposée d’elle-même suite à un flash. Sa réalisation s’est faite manuellement par une succession de copier-coller depuis le tableau des pourcentages.
La simulation de la solution s’est donc construite au fil d’une réflexion qui a créé les conditions favorables à l’apparition d’un flash.
Flash : En recherche de solution, tous les sens du développeur sont en alerte. Sa réflexion fouille, tente, fait des liens, jusqu’à ce qu’une idée s’invite par surprise. Pas nécessairement attendue ou espérée, cette idée est la bienvenue, mais elle peut se faire attendre très longtemps et même ne jamais se manifester. Quand elle arrive, elle vient apparemment de nulle part ou du fin fond de sa mémoire procédurale. Elle survient en fait à la suite d’une convergence inopinée de soft skills comme la logique, la créativité, l’intuition, une coïncidence, voire même la chance. Un flash s’accompagne d’un instant émotionnel fort qui stabilise toutes les idées qui étaient en germe.
NB : N’ayant aucune compétence python, ce billet ne propose pas de programmation codée.
■ § 1. Homogénéiser la répartition d’un tableau
■ § 1.1. La problématique
Bonjour,
D'avance merci de l'attention que vous porterez à ce problème. Je suis nul en algorithme mais pour un développeur ce problème est trivial. Je cherche à programmer en Python un script qui produit une Playlist.
Cette Playlist contient des titres de genres musicaux différents (rock, hiphop, musique française, reggae, etc.). Ces genres musicaux ne sont pas tous présents en même proportion : sur la Playlist (il y a 34% de musique française, 33% de rock, 12% de hiphop, 7% de reggae, etc.).
Je voudrais que mon programme génère une Playlist telle que la répartition des genres soit homogène.
Exemple :
- Si j'ai 33% de rock, alors j'aurai un titre rock tous les 3 titres.
- Si j'ai 7% de reggae, alors j'aurai un reggae à peu près tous les 14 titres.
Pour simplifier on peut comparer mon problème à celui-ci plus simple :
On a 100 jetons de 5 couleurs différentes. On a un tableau de 100 cases. Comment répartir dans le tableau les jetons de couleurs différentes de la façon la plus homogène possible ?
Exemple :
- 50 jetons verts
- 30 jetons rouges
- 10 jetons bleus
- 7 jetons jaunes
- 3 jetons noirs
On peut calculer facilement la fréquence d'un jeton de chaque couleur :
| fr(vert) |
= 100/50 |
= 2 |
=> un jeton tous les 2 jetons |
| fr(rouge) |
= int(100/30) + 100mod30 |
= 3 reste 10 |
=> un jeton tous les 3 jetons |
| fr(bleus) |
= 100/10 |
= 10 |
=> un jeton tous les 10 jetons |
| fr(jaune) |
= int(100/7) + 100mod7 |
= 14 reste 2 |
=> un jeton tous les 14 jetons |
| fr(noir) |
= int(100/3) + 100mod3 |
= 33 reste 1 |
=> un jeton tous les 33 jetons |
- Comment construire un tableau qui respecte ces fréquences le mieux possible ?
- Que faire des restes ?
- Comment traiter le cas où des jetons de différentes couleurs tombent sur la même case du tableau ?
C'est trop complexe pour ma petite tête, je m'y perds.
Merci de m'aider.
petit_chat
|
■ § 1.2. La pédagogie "Inspecteur Colombo"
On a donc 100 jetons de 5 couleurs différentes correspondant à des genres musicaux différents.
Comment répartir ces jetons en proportions différentes dans une Playlist de genres musicaux la plus homogène possible ?
- 50 jetons verts (variété française)
- 30 jetons rouges (rock)
- 10 jetons bleus (hiphop)
- 7 jetons jaunes (reggae)
- 3 jetons noirs (musique de film)
Ma réflexion s’appuie sur l’exemple de petit_chat mais ma démarche ne pourrait pas s’appliquer pour un pourcentage supérieur à 50%... Sauf à dédoubler ce pourcentage : 50% d’une part, et le pourcentage restant d’autre part. Rien n’empêche en effet de déclarer deux pourcentages de jetons de même couleur. Ainsi, les 10 jetons bleus pourraient être verts et porter le pourcentage des jetons verts (variété française) à 60%.
Prenons cet exemple de petit_chat comme un exercice d’algorithmique.
La solution nécessite à priori deux algorithmes :
- Un premier algorithme pour affecter les jetons dans un tableau en deux dimensions de 100 liges sur 5 colonnes, soit une colonne par genre musical (Cf. Tableau Excel "Pourcentages") :
- Soit un algorithme appliqué à un tableau en deux dimensions
- Soit un algorithme appliqué à une table BDD
- Un second algorithme pour créer la Playlist à partir du tableau "Pourcentages" (Cf. Tableau Excel "Playlist")
Avant d’aller plus loin, je vous montre d’abord le résultat de ma réflexion à l’aide de deux tableaux Excel, puis je vous explique.
Ces deux tableaux résultent d’une simple simulation. C’est juste de la réflexion pragmatique, il n’est pas encore question d’algorithmique.
Attention !
Excel permettant d’utiliser la couleur, un jeton peut être représenté à la fois par une cellule de couleur et le chiffre "1". Les totalisations verticales et horizontales valident ainsi l’algorithme utilisé à base de calculs.
Sans la couleur, la Playlist (2ème tableau Excel), n’afficherait qu’une liste de "1" inexploitable.
La programmation ne permettant pas d’utiliser la couleur, il faudra bien à un moment ou à un autre, concrétiser les jetons par le libellé ou le code de leur couleur.
Cela peut se faire dès le premier algorithme mais pour cet exercice, c’est le 2ème algorithme qui s’en charge.
■ § 2. Tableaux Excel
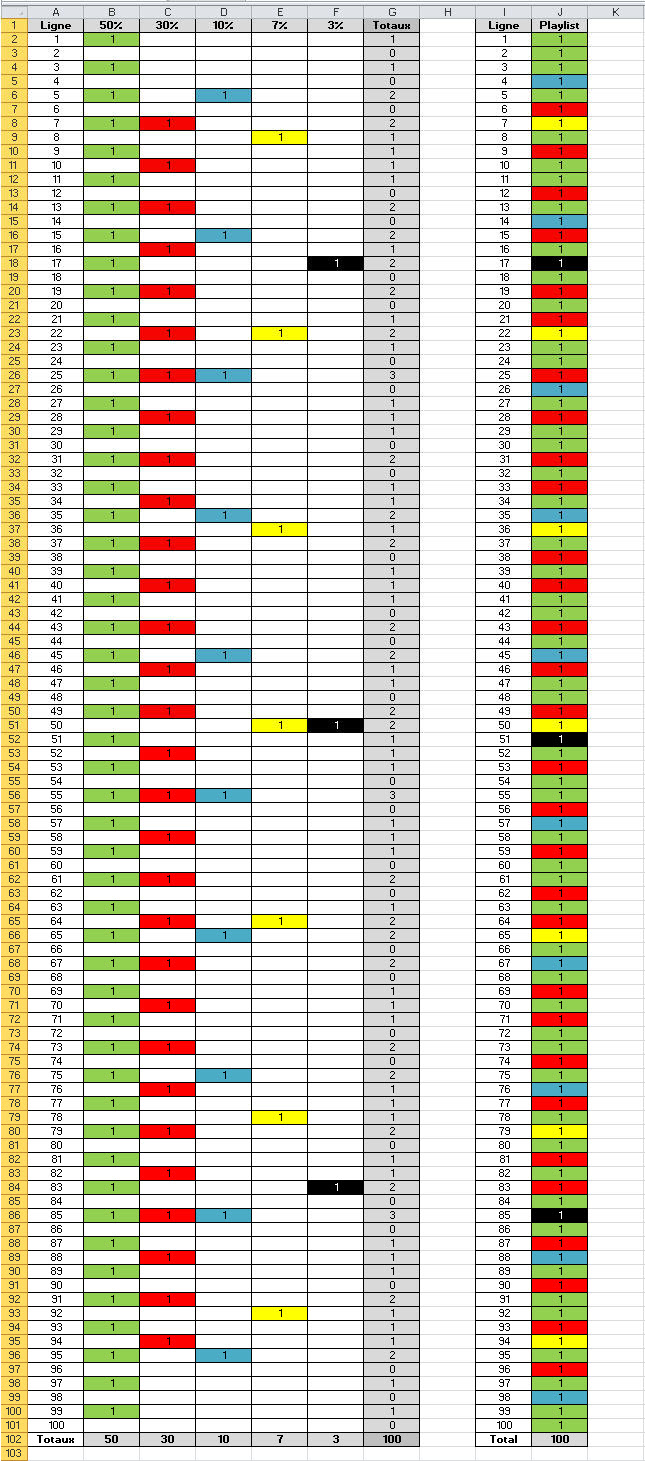
- Le premier tableau "Pourcentages" (matrice 100 x 5) correspond au 1er algorithme.
Les jetons sont placés manuellement en fonction des intervalles propres à chaque pourcentage.
Certaines lignes ont deux voire trois jetons de couleurs différentes quand d’autres lignes n’en n’ont aucun. C’est normal. Globalement il y en a 100.
(§ 4. Homogénéisation des pourcentages).
- Le deuxième tableau "Playlist" correspond au 2ème algorithme.
Le tableau "Pourcentages" étant parcouru horizontalement de la gauche vers la droite et verticalement de la première à la dernière ligne, les cellules avec jeton sont copiées-collées chronologiquement dans la "Playlist".
■ § 3. Simulation
■ § 3.1. Identification des données
Ce n’est finalement qu’un problème d’intervalles.
L’algorithmique, c’est de la réflexion, de l’observation, de la logique, de la simulation avec trois outils : un crayon, une gomme et une feuille de papier.
Le crayon commence par s’intéresser au pourcentage, 10% par exemple, trace une ligne horizontale représentant 100% et la découpe à l’aide de traits verticaux en 10 parts égales. Surprise ! Il n’y a que 9 traits.
C’est là que la calculette s’invite comme 4ème outil.
Pour connaitre l’intervalle entre deux traits, il faut donc soustraire les dix traits verticaux de 100 et diviser le résultat (90) par le nombre de traits verticaux (10) pour avoir 9 intervalles identiques.
Résultat : l’intervalle = 9
Vérification :
10 traits verticaux + 9 intervalles de 9 = 91
Il reste donc 100 - 91 = 9 que l’on peut diviser par 2 pour affecter un espace avant le premier trait (4) et un espace après le dernier trait (5).
Nouveau test :
Le crayon trace une nouvelle ligne horizontale pour visualiser le pourcentage 3%... Et ça fonctionne de la même façon.
Et avec 50% ça se passe comment ?
Reste = 1
Reste / 2 = 0 (espace avant le premier trait vertical) et Reste - 0 = 1 (espace après le dernier trait vertical)… Normal.
Visuel :
┌────────────────> N° de ligne (1 à 100)
│
│ ┌────────────> Pourcentage (50, 30, 10, 7, 3)
┌─┴─┬─┴─┐
│ N°│NB%│
├───┼───┤ ──┐
│ 1│ │ │
├───┼───┤ ├────> Cellules-Avant (sans jetons)
│ 2│ │ │
├───┼───┤ ──┴─────────────────────────────────────────────────┐
│ 3│ 1 │ ──────> 1ère Cellule avec jeton │
├───┼───┤ ──┐ │
│ 4│ │ │ │
├───┼───┤ │ │
│ 5│ │ ├───> Cellules-Intervalle ──┐ │
├───┼───┤ │ (sans jetons) │ │
│ 6│ │ │ │ │
├───┼───┤ ──┘ │ │
│ 7│ 1 │ ├─> Total-Intervalles ├─> Cellules-Début-Fin
├───┼───┤ ──┐ │ │
│ 8│ │ │ │ │
├───┼───┤ │ │ │
│ 9│ │ ├───> Cellules-Intervalle ──┘ │
├───┼───┤ │ (sans jetons) │
│ 10│ │ │ │
├───┼───┤ ──┘ │
│ 11│ 1 │ ──────> dernière Cellule avec jeton │
├───┼───┤ ──┬─────────────────────────────────────────────────┘
│ 12│ │ │
├───┼───┤ ├────> Cellules-Après (sans jetons)
│ 13│ │ │
└───┴───┘ ──┘
■ § 3.2. Les données et leur calcul
Entre le premier et le dernier jeton il y a autant d’intervalles (avec le même nombre de cellules) que de jetons moins un.
Le calcul de l’intervalle occasionne toujours un reste à répartir pour moitié avant le premier jeton et pour autre moitié après le dernier jeton.
L'espace avant le premier jeton correspond à 100 moins le nombre de cellules entre le 1er et le dernier jeton (Cellules_Début-Fin) divisé par 2 (on ne considère que les entiers).
L'espace après le dernier jeton correspond au reste de cette division par 2. Ce reste est ce qu’il est, il ne sera pas forcément égal à l'espace avant le premier jeton mais il n’est pas nécessaire de le connaitre.
Définition |
Mnémonique |
Calcul |
|---|
| N° de ligne |
N° |
De 1 à n |
| Pourcentage |
NB% |
NB% = 50, 30, 10, 7, ou 3 |
| Nombre total de cellules sans jeton |
Cellules_vides |
100 - NB% |
| Nombre de cellules sans jeton entre deux cellules avec jeton |
Cellules_Intervalle |
Cellules_Vides / NB% |
| Total des cellules vides entre la 1ère cellule avec jeton et la dernière cellule avec jeton |
Total_Intervalles |
Cellules_Intervalle * (NB% - 1) |
| Total des cellules entre la 1ère cellule avec jeton et la dernière cellule avec jeton |
Cellules_Début-Fin |
NB% + Total_Intervalles |
| Cellules avant la 1ère cellule avec jeton et après la dernière cellule avec jeton |
Cellules_Restantes |
100 - Cellules_Début-Fin |
| Nombre de cellules sans jeton avant la 1ère cellule avec jeton |
Cellules_Avant |
Cellules_Restantes / 2 |
| Nombre de cellules sans jeton après la dernière cellule avec jeton |
Cellules_Après |
Cellules_Restantes - Cellules_Avant |
■ § 4. Homogénéisation des pourcentages
■ § 4.1. Calcul des intervalles 50% jetons verts
| Données |
Formule |
Calculs JETONS VERTS |
Résultat |
|---|
| NB% |
NB% = 50, 30, 10, 7 ou 3 |
50 |
50 |
| Cellules_Vides |
100 - NB% |
100 - 50 |
50 |
| Cellules_Intervalle |
Cellules_Vides / NB% |
50 / 50 |
1 |
| Total_Intervalles |
Cellules_Intervalle * (NB% - 1) |
1 * (50 - 1) |
49 |
| Cellules_Début-Fin |
NB% + Total_Intervalles |
50 + 49 |
99 |
| Cellules_Restantes |
100 - Cellules_Début-Fin |
100 - 99 |
1 |
| Cellules_Avant |
Cellules_Restantes / 2 |
1 / 2 |
0 |
| Cellules_Après |
Cellules_Restantes - Cellules_Avant |
1 - 0 |
1 |
■ § 4.2. Calcul des intervalles 30% jetons rouges
| Données |
Formule |
Calculs JETONS ROUGES |
Résultat |
|---|
| NB% |
NB% = 50, 30, 10, 7 ou 3 |
30 |
30 |
| Cellules_Vides |
100 - NB% |
100 - 30 |
70 |
| Cellules_Intervalle |
Cellules_Vides / NB% |
70 / 30 |
2 |
| Total_Intervalles |
Cellules_Intervalle * (NB% - 1) |
2 * (30 - 1) |
58 |
| Cellules_Début-Fin |
NB% + Total_Intervalles |
30 + 58 |
88 |
| Cellules_Restantes |
100 - Cellules_Début-Fin |
100 - 88 |
12 |
| Cellules_Avant |
Cellules_Restantes / 2 |
12 / 2 |
6 |
| Cellules_Après |
Cellules_Restantes - Cellules_Avant |
12 - 6 |
6 |
■ § 4.3. Calcul des intervalles 10% jetons bleus
| Données |
Formule |
Calculs JETONS BLEUS |
Résultat |
|---|
| NB% |
NB% = 50, 30, 10, 7 ou 3 |
10 |
10 |
| Cellules_Vides |
100 - NB% |
100 - 10 |
90 |
| Cellules_Intervalle |
Cellules_Vides / NB% |
90 / 10 |
9 |
| Total_Intervalles |
Cellules_Intervalle * (NB% - 1) |
9 * (10 - 1) |
81 |
| Cellules_Début-Fin |
NB% + Total_Intervalles |
10 + 81 |
91 |
| Cellules_Restantes |
100 - Cellules_Début-Fin |
100 - 91 |
9 |
| Cellules_Avant |
Cellules_Restantes / 2 |
9 / 2 |
4 |
| Cellules_Après |
Cellules_Restantes - Cellules_Avant |
9 - 4 |
5 |
■ § 4.4. Calcul des intervalles 7% jetons jaunes
| Données |
Formule |
Calculs JETONS JAUNES |
Résultat |
|---|
| NB% |
NB% = 50, 30, 10, 7 ou 3 |
7 |
7 |
| Cellules_Vides |
100 - NB% |
100 - 7 |
93 |
| Cellules_Intervalle |
Cellules_Vides / NB% |
93 / 7 |
13 |
| Total_Intervalles |
Cellules_Intervalle * (NB% - 1) |
13 * (7 - 1) |
78 |
| Cellules_Début-Fin |
NB% + Total_Intervalles |
7 + 78 |
85 |
| Cellules_Restantes |
100 - Cellules_Début-Fin |
100 - 85 |
15 |
| Cellules_Avant |
Cellules_Restantes / 2 |
15 / 2 |
7 |
| Cellules_Après |
Cellules_Restantes - Cellules_Avant |
15 - 7 |
8 |
■ § 4.5. Calcul des intervalles 3% jetons noirs
| Données |
Formule |
Calculs JETONS NOIRS |
Résultat |
|---|
| NB% |
NB% = 50, 30, 10, 7 ou 3 |
3 |
3 |
| Cellules_Vides |
100 - NB% |
100 - 3 |
97 |
| Cellules_Intervalle |
Cellules_Vides / NB% |
97 / 3 |
32 |
| Total_Intervalles |
Cellules_Intervalle * (NB% - 1) |
32 * (3 - 1) |
64 |
| Cellules_Début-Fin |
NB% + Total_Intervalles |
3 + 64 |
67 |
| Cellules_Restantes |
100 - Cellules_Début-Fin |
100 - 67 |
33 |
| Cellules_Avant |
Cellules_Restantes / 2 |
33 / 2 |
16 |
| Cellules_Après |
Cellules_Restantes - Cellules_Avant |
33 - 16 |
17 |
NB : Après positionnement des jetons dans chaque colonne, certaines lignes comptabilisent jusqu’à trois jetons alors que d’autres lignes n’en n’ont aucun. C’est le 2ème algorithme qui résout cette situation.
■ § 5. Homogénéisation de la Playlist via une matrice (100 x 5)
■ § 5.1. Algorigramme pour renseigner une matrice
Les variables
| ÉLÉMENT_MATRICIE |
= Élément Matriciel correspondant à une cellule du 1er tableau Excel |
| NB_COLONNES |
= Nombre de Colonnes (5) |
| NB_JETONS |
= Nombre de Jetons (Pourcentage : 50, 30, 10, 7, 3) |
| CTR_JETONS |
= Compteur de Jetons |
| I_LIGNE |
= Index Ligne |
| I_COLONNE |
= Index Colonne |
| I_INTERVALLE |
= Index Intervalle |
L'algorigramme
┌───────────────────────────────────────────────────────┐
D_PROG │ NB_COLONNES = 5 │
│ I_COLONNE = 0 │
└───────────────────────────┬───────────────────────────┘
│◄──────────────────────────────────────┐
┌───────────────────────────┴───────────────────────────┐ │
D_COLONNE │ 100 - NB% (ex. : NB% = 50) = Cellules_Vides │ │
│ Cellules_Vides / NB% = Cellules_Intervalle │ │
│ Cellules_Intervalle * (NB% - 1) = Total_Intervalles │ │
│ NB% + Total_intervalles = Cellules_Début-Fin │ │
│ 100 - Cellules_Début-Fin = Cellules_Après │ │
│ Cellules_restantes / 2 = Cellules_Avant │ │
├───────────────────────────────────────────────────────┤ │
│ I_COLONNE = I-COLONNE + 1 │ │
│ I_LIGNE = 0 │ │
│ CTR_JETONS = 0 │ │
└───────────────────────────┬───────────────────────────┘ │
│◄──────────────────────────────┐ │
┌───────────────────────────┴───────────────────────────┐ │ │
T_AVANT │ I_LIGNE = I_LIGNE + 1 │ │ │
│ I_LIGNE :: Cellules_Avant │ │ │
└───────────────────────────┬───────────────────────────┘ < │ │
●───────────────────────────────┘ │
│◄──────────────────────────────────┐ │
┌───────────────────────────┴───────────────────────────┐ │ │
D_JETON │ ÉLÉMENT_MATRICIEL (I_LIGNE, I_COLONNE) = "1" │ │ │
│ CTR_JETONS = CTR_JETONS + 1 │ │ │
│ I_INTERVALLE = 0 │ │ │
└───────────────────────────┬───────────────────────────┘ │ │
│◄──────────────────────────────┐ │ │
┌───────────────────────────┴───────────────────────────┐ │ │ │
T_INTERVALLE │ I_LIGNE = I_LIGNE + 1 │ │ │ │
│ I_INTERVALLE = I_INTERVALLE + 1 │ │ │ │
│ I_INTERVALLE :: Cellules_Intervalle │ │ │ │
└───────────────────────────┬───────────────────────────┘ < │ │ │
●───────────────────────────────┘ │ │
┌───────────────────────────┴───────────────────────────┐ │ │
F_JETON │ CTR_JETONS :: (NB_JETONS - 1) │ │ │
└───────────────────────────┬───────────────────────────┘ < │ │
●───────────────────────────────────┘ │
┌───────────────────────────┴───────────────────────────┐ │
F_COLONNE │ ÉLÉMENT_MATRICIEL (I_LIGNE, I_COLONNE) = "1" │ │
│ I_COLONNE :: NB_COLONNES │ │
└───────────────────────────┬───────────────────────────┘ < │
●───────────────────────────────────────┘
┌───────────────────────────┴───────────────────────────┐
F_PROG │ Ø │
└───────────────────────────────────────────────────────┘
■ § 5.2. Algorigramme pour créer la Playlist depuis une matrice
Il suffit de lire chaque ligne de la matrice de la gauche vers la droite en parcourant la matrice verticalement de la première à la dernière ligne et de reporter chronologiquement chaque jeton (son libellé ou son code) dans la Playlist.
Les variables de la matrice (100 lignes x 5 colonnes)
| ÉLÉMENT_MATRICIEL |
= Élément Matriciel |
| I_LIGNE |
= Index Ligne |
| K_LIGNE |
= Index Borne Ligne |
| I_COLONNE |
= Index Colonne |
| K_COLONNE |
= Index Borne Colonne (5) |
| JETON |
= Couleur du jeton ("V", "R", "B", "J", "N") |
Les variables de la Table Playlist (100 lignes)
| I_PLAYLIST |
= Index Playlist |
L'Algorigramme
┌───────────────────────────────────────────────────────┐
D_PROG │ I_LIGNE = 0 │
│ K_LIGNE = 100 │
│ I_COLONNE = 0 │
│ K_COLONNE = 5 │
│ I_PLAYLIST = 0 │
└───────────────────────────┬───────────────────────────┘
│◄────────────────────────────────────┐
┌───────────────────────────┴───────────────────────────┐ │
D_LIGNE │ I_LIGNE = I_LIGNE + 1 │ │
│ I_COLONNE = 0 │ │
│ JETON = "" │ │
└───────────────────────────┬───────────────────────────┘ │
│◄───────────────────────────────┐ │
┌───────────────────────────┴───────────────────────────┐ │ │
D_COLONNE │ I_COLONNE = I_COLONNE + 1 │ │ │
│ I_COLONNE :: 1 │ │ │
└───────────────────────────┬───────────────────────────┘ │ │
NULL ┌──────────────●──────────────┐ = │ │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ Ø │ │ JETON = "V" │ │ │
└────────────┬────────────┘ └────────────┬────────────┘ │ │
└──────────────┬──────────────┘ │ │
┌───────────────────────────┴───────────────────────────┐ │ │
│ I_COLONNE :: 2 │ │ │
└───────────────────────────┬───────────────────────────┘ │ │
NULL ┌──────────────●──────────────┐ = │ │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ Ø │ │ JETON = "R" │ │ │
└────────────┬────────────┘ └────────────┬────────────┘ │ │
└──────────────┬──────────────┘ │ │
┌───────────────────────────┴───────────────────────────┐ │ │
│ I_COLONNE :: 3 │ │ │
└───────────────────────────┬───────────────────────────┘ │ │
NULL ┌──────────────●──────────────┐ = │ │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ Ø │ │ JETON = "B" │ │ │
└────────────┬────────────┘ └────────────┬────────────┘ │ │
└──────────────┬──────────────┘ │ │
┌───────────────────────────┴───────────────────────────┐ │ │
│ I_COLONNE :: 4 │ │ │
└───────────────────────────┬───────────────────────────┘ │ │
NULL ┌──────────────●──────────────┐ = │ │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ Ø │ │ JETON = "J" │ │ │
└────────────┬────────────┘ └────────────┬────────────┘ │ │
└──────────────┬──────────────┘ │ │
┌───────────────────────────┴───────────────────────────┐ │ │
│ I_COLONNE :: 5 │ │ │
└───────────────────────────┬───────────────────────────┘ │ │
NULL ┌──────────────●──────────────┐ = │ │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ Ø │ │ JETON = "N" │ │ │
└────────────┬────────────┘ └────────────┬────────────┘ │ │
└──────────────┬──────────────┘ │ │
┌───────────────────────────┴───────────────────────────┐ │ │
│ ÉLÉMENT_MATRICIEL (I_LIGNE, I_COLONNE) :: "1" │ │ │
└───────────────────────────┬───────────────────────────┘ │ │
NULL ┌──────────────●──────────────┐ = │ │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
T_ELEMENT_MATRICIEL │ │ │ I_PLAYLIST = I_PLAYLIST │ │ │
│ Ø │ │ + 1 │ │ │
│ │ │ Print I_PLAYLIST, " = ",│ │ │
│ │ │ JETON │ │ │
└────────────┬────────────┘ └────────────┬────────────┘ │ │
└──────────────┬──────────────┘ │ │
┌───────────────────────────┴───────────────────────────┐ │ │
F_COLONNE │ I_COLONNE :: K_COLONNE │ │ │
└───────────────────────────┬───────────────────────────┘ < │ │
●────────────────────────────────┘ │
┌───────────────────────────┴───────────────────────────┐ │
F_LIGNE │ I_LIGNE :: K_LIGNE │ │
└───────────────────────────┬───────────────────────────┘ < │
●─────────────────────────────────────┘
┌───────────────────────────┴───────────────────────────┐
F_PROG │ Ø │
└───────────────────────────────────────────────────────┘
■ § 6. Homogénéisation de la Playlist via une BDD
■ § 6.1. Algorigramme pour créer une table "couleur" BDD
Le programme doit être exécuté pour chaque couleur. Les 5 tables couleurs étant créées, il reste à concaténer ces 5 tables en une seule via des requêtes SQL. Chaque table doit être constituée de tous les N° de ligne avec ou sans jeton.
Cette table unique pourra être traitée comme le tableau en deux dimensions pour réaliser une liste séquentielle des jetons de couleurs.
Création de la table t_couleur
Après création de cette table pour une couleur, une requête SQL copie t_couleur.j_couleur dans l’attribut correspondant de la table t_jetons (
j_vert, j_rouge, j_bleu, j_jaune ou j_noir).
{ t_couleur (table couleur) ---------------------------------------------------}
create table t_couleur
(
n_ligne integer not null,
j_couleur char(1)
) ;
{------------------------------------------------------------------------------}
| JETON |
= Couleur du jeton ("V", "R", "B", "J", "N") |
| NB_JETON |
= Nombre de Jetons (Pourcentage : 50, 30, 10, 7, 3) |
| CTR_JETON |
= Compteur de Jetons |
| I_LIGNE |
= Index Ligne |
| I_COLONNE |
= Index Colonne |
| I_INTERVALLE |
= Index Intervalle |
| SÉPARATEUR |
= "ǀ" (pipe) |
La requête SQL pour la couleur verte
{------------------------------------------------------------------------------}
update t_jetons
set t_jetons.j_vert = (select t_couleur.j_couleur
from t_couleur
where t_couleur.ligne = t_jetons.ligne)
where t_couleur.ligne = t_jetons.ligne ;
{------------------------------------------------------------------------------}
┌───────────────────────────────────────────────────────┐
D_PROG │ 100 - NB% (ex. : NB% = 50) = Cellules_Vides │
│ Cellules_Vides / NB% = Cellules_Intervalle │
│ Cellules_Intervalle * (NB% - 1) = Total_Intervalles │
│ NB% + Total_intervalles = Cellules_Début-Fin │
│ 100 - Cellules_Début-Fin = Cellules_Après │
│ Cellules_restantes / 2 = Cellules_Avant │
├───────────────────────────────────────────────────────┤
│ JETON = V, R, B, J, ou N │
│ NB_JETONS = 50, 30 10, 7, 3 │
│ CTR_JETONS = 0 │
│ I_LIGNE = 1 │
└───────────────────────────┬───────────────────────────┘
│◄───────────────────────────────┐
┌───────────────────────────┴───────────────────────────┐ │
D_LIGNE │ I_LIGNE = I_LIGNE + 1 │ │
│ I_LIGNE :: Cellules_Avant │ │
└───────────────────────────┬───────────────────────────┘ │
┌──────────────●──────────────┐ │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │
T_AVANT │ Ø │ │ PRINT I_LIGNE, "ǀǀ" │ │
└────────────┬────────────┘ └────────────┬────────────┘ │
└──────────────┬──────────────┘ │
┌───────────────────────────┴───────────────────────────┐ │
│ I_LIGNE :: Cellules_Avant │ │
└───────────────────────────┬───────────────────────────┘ < │
●────────────────────────────────┘
│◄──────────────────────────────────┐
┌───────────────────────────┴───────────────────────────┐ │
T_JETON │ PRINT I_LIGNE, "ǀ", "JETON", "ǀ" │ │
│ CTR_JETONS = CTR_JETONS + 1 │ │
│ I_INTERVALLE = 0 │ │
└───────────────────────────┬───────────────────────────┘ │
│◄──────────────────────────────┐ │
┌───────────────────────────┴───────────────────────────┐ │ │
T_INTERVALLE │ PRINT I_LIGNE, "ǀ", "ǀ" │ │ │
│ I_INTERVALLE = I_INTERVALLE + 1 │ │ │
│ I_INTERVALLE :: Cellules_Intervalle │ │ │
└───────────────────────────┬───────────────────────────┘ < │ │
●───────────────────────────────┘ │
┌───────────────────────────┴───────────────────────────┐ │
F_JETON │ CTR_JETONS :: (NB_JETONS - 1) │ │
└───────────────────────────┬───────────────────────────┘ < │
●───────────────────────────────────┘
┌───────────────────────────┴──────────────────────────┐
INTER │ PRINT I_LIGNE, "ǀ", JETON, "ǀ" │
└───────────────────────────┬──────────────────────────┘
│◄──────────────────────────────┐
┌───────────────────────────┴───────────────────────────┐ │
D_APRES │ I_LIGNE = I_LIGNE + 1 │ │
│ I_LIGNE :: NB_LIGNES │ │
└───────────────────────────┬───────────────────────────┘ │
= ┌──────────────●──────────────┐ < │
┌────────────┴────────────┐ ┌────────────┴────────────┐ │
T_APRES │ Ø │ │ PRINT I_LIGNE, "ǀ", "ǀ" │ │
└────────────┬────────────┘ └────────────┬────────────┘ │
└──────────────┬──────────────┘ │
┌───────────────────────────┴───────────────────────────┐ │
F_APRES │ I_LIGNE :: NB_LIGNES │ │
└───────────────────────────┬───────────────────────────┘ < │
●───────────────────────────────┘
┌───────────────────────────┴───────────────────────────┐
F_PROG │ Ø │
└───────────────────────────────────────────────────────┘
■ § 6.2. Algorigramme pour créer la Playlist depuis une table BDD
Il suffit de lire chaque item de la table BDD (t_jetons), de tester chaque attribut (j_vert, j_rouge, j_bleu, j_jaune, j_noir) et de reporter chronologiquement chaque jeton dans la Playlist.
Création de la table t_jetons
{ t_jetons (table jetons) -----------------------------------------------------}
create table t_jetons
(
n_ligne integer not null,
j_vert char(1),
j_rouge char(1),
j_bleu char(1),
j_jaune char(1),
j_noir char(1)
) ;
{------------------------------------------------------------------------------}
| T_JETONS |
= Table des Jetons |
| I_LIGNE |
= Index Ligne |
| K_LIGN |
= Index Playlist |
Les variables de la Table Playlist (100 lignes)
| I_PLAYLIST |
= Index Playlist |
L'Algorigramme
┌───────────────────────────────────────────────────────┐
D_PROG │ I_LIGNE = 0 │
│ K_LIGNE = 100 │
│ I_PLAYLIST = 0 │
└───────────────────────────┬───────────────────────────┘
│◄────────────────────────────────────┐
┌───────────────────────────┴───────────────────────────┐ │
D_ITEM │ I_LIGNE = I_LIGNE + 1 │ │
└───────────────────────────┬───────────────────────────┘ │
┌────────────────────────────────┼────────────────────────────────┐ │
│ ┌───────────────────────────┴───────────────────────────┐ │ │
T_ITEM │ │ j_vert :: "V" │ │ │
│ └───────────────────────────┬───────────────────────────┘ │ │
│ NULL ┌──────────────●──────────────┐ = │ │
│ ┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ │ │ │ I_PLAYLIST = I_PLAYLIST │ │ │
│ │ Ø │ │ + 1 │ │ │
│ │ │ │ Print I_PLAYLIST, "ǀBǀ" │ │ │
│ └────────────┬────────────┘ └────────────┬────────────┘ │ │
│ └──────────────┬──────────────┘ │ │
│ ┌───────────────────────────┴───────────────────────────┐ │ │
│ │ j_rouge :: "R" │ │ │
│ └───────────────────────────┬───────────────────────────┘ │ │
│ NULL ┌──────────────●──────────────┐ = │ │
│ ┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ │ │ │ I_PLAYLIST = I_PLAYLIST │ │ │
│ │ Ø │ │ + 1 │ │ │
│ │ │ │ Print I_PLAYLIST, "ǀRǀ" │ │ │
│ └────────────┬────────────┘ └────────────┬────────────┘ │ │
│ └──────────────┬──────────────┘ │ │
│ ┌───────────────────────────┴───────────────────────────┐ │ │
│ │ j_bleu :: "B" │ │ │
│ └───────────────────────────┬───────────────────────────┘ │ │
│ NULL ┌──────────────●──────────────┐ = │ │
│ ┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ │ │ │ I_PLAYLIST = I_PLAYLIST │ │ │
│ │ Ø │ │ + 1 │ │ │
│ │ │ │ Print I_PLAYLIST, "ǀBǀ" │ │ │
│ └────────────┬────────────┘ └────────────┬────────────┘ │ │
│ └──────────────┬──────────────┘ │ │
│ ┌───────────────────────────┴───────────────────────────┐ │ │
│ │ j_jaune :: "J" │ │ │
│ └───────────────────────────┬───────────────────────────┘ │ │
│ NULL ┌──────────────●──────────────┐ = │ │
│ ┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ │ │ │ I_PLAYLIST = I_PLAYLIST │ │ │
│ │ Ø │ │ + 1 │ │ │
│ │ │ │ Print I_PLAYLIST, "ǀJǀ" │ │ │
│ └────────────┬────────────┘ └────────────┬────────────┘ │ │
│ └──────────────┬──────────────┘ │ │
│ ┌───────────────────────────┴───────────────────────────┐ │ │
│ │ j_noir :: "N" │ │ │
│ └───────────────────────────┬───────────────────────────┘ │ │
│ NULL ┌──────────────●──────────────┐ = │ │
│ ┌────────────┴────────────┐ ┌────────────┴────────────┐ │ │
│ │ │ │ I_PLAYLIST = I_PLAYLIST │ │ │
│ │ Ø │ │ + 1 │ │ │
│ │ │ │ Print I_PLAYLIST, "ǀNǀ" │ │ │
│ └────────────┬────────────┘ └────────────┬────────────┘ │ │
│ └──────────────┬──────────────┘ │ │
└────────────────────────────────┼────────────────────────────────┘ │
┌───────────────────────────┴───────────────────────────┐ │
F_ITEM │ I_LIGNE :: K_LIGNE │ │
└───────────────────────────┬───────────────────────────┘ < │
●─────────────────────────────────────┘
┌───────────────────────────┴───────────────────────────┐
F_PROG │ Ø │
└───────────────────────────────────────────────────────┘
■ § 7. Conclusion
Dans l’énoncé de sa problématique, petit_chat pose les questions :
- On a un tableau de 100 cases. Comment répartir dans le tableau les jetons de couleurs différentes de la façon la plus homogène possible ?
- Comment traiter le cas où des jetons de différentes couleurs tombent sur la même case du tableau ?
Son tableau modélise sa Playlist, en fait une table de 100 items qu’il cherche à implémenter par un algorithme miraculeux.
Spécialistes de "La Logique Combinatoire", les intervenants dans la discussion qu’il a initiée, ont tenté tant bien que mal de faire la même chose, concevoir un algorithme unique (un programme), à coups de suppositions (Sept messages comportent une dizaine de conditions « Si… »), de conseils, de difficultés à prévoir et de bouts de code.
Mais pour résoudre rationnellement cette problématique, il fallait comprendre que la solution nécessitait deux algorithmes :
- Un premier algorithme pour homogénéiser les jetons de même couleur selon leur pourcentage dans un tableau de 100 lignes sur 5 colonnes, soit une colonne par genre musical.
- Un second algorithme pour créer la Playlist à partir de ce tableau.
Le tableau des Pourcentages terminé, y accoler une Playlist vide s’imposait naturellement.
100 jetons de différentes couleurs dans le tableau des Pourcentages et 100 cases vides dans la Playlist… La façon de remplir cette Playlist vide devient évidente : copier-coller chronologiquement les jetons, les jetons de même rang ne contrariant en rien l’objectif :
- Générer une Playlist telle que la répartition des genres soit homogène.
Au final, la répartition des jetons de couleur dans la Playlist est la plus homogène possible. Au pire, par rapport au placement idéal des jetons dans le tableau des Pourcentages, un jeton de la Playlist peut être décalé de un, quelque fois deux et exceptionnellement trois rangs.
FIN - Exercice corrigé d’algorithmique (Force 5/7)
Homogénéiser la répartition d'un tableau

![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog Viadeo](https://forum.developpez.be/images/misc/bookmarksite_viadeo.gif)
![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog Twitter](https://forum.developpez.be/images/misc/bookmarksite_twitter.png)
![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog Google](https://forum.developpez.be/images/misc/bookmarksite_google.gif)
![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog Facebook](https://forum.developpez.be/images/misc/bookmarksite_facebook.gif)
![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog Digg](https://forum.developpez.be/images/misc/bookmarksite_digg.gif)
![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog Delicious](https://forum.developpez.be/images/misc/bookmarksite_delicious.gif)
![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog MySpace](https://forum.developpez.be/images/misc/bookmarksite_myspace.gif)
![Envoyer le billet « [TUTORIEL] Homogénéiser la répartition d'un tableau » dans le blog Yahoo](https://forum.developpez.be/images/misc/bookmarksite_yahoo.gif)


