Problème de géométrie

**BBric** · 31/01/2024, 23h05

Bonjour, j'ai un petit problème de géométrie, si ça se trouve c'est super simple, mais je ne vois pas.

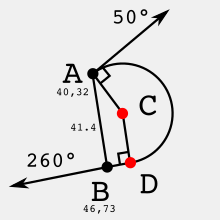
Je voudrais connaître les coordonnées du centre du cercle qui passe par A et D. Le rayon AC est perpendiculaire à la tangente 50°, et le rayon CD à la tangente 260°.

Nom : temp.png
Affichages : 101
Taille : 23,3 Ko

Nom : temp.png
Affichages : 101
Taille : 23,3 Ko

**Alex64** · 01/02/2024, 11h09

bonjour bbric

que vient faire le point B, est-il utile pour résoudre ce problème ???
1) le système de coordonnées doit être changé : B(0 ; 0) et A(-6 ; 41 ) par exemple
2) l'angle de 270° devient : 190°
la tangente au cercle en D passe-t-elle par B ??? si oui => le problème est solvable avec 1) et 2) !! => xC=11.966 yC = 25.9247
NB j'ai remarqué que AB n'est pas parallèle au vecteur CD !!!

**Stellar7** · 01/02/2024, 20h43

Bonjour,

Comme @Alex64, je ne suis pas sûr, au premier abord, de l'intérêt du point B. En deuxième r'abord, comme il le suggère, ben c'est pas top. C'est peut-être pour brouiller l'écoute du lecteur ? (oui, contrepèterie assumée)

Bon, une droite, c'est y=ax+b. Le "a", c'est la pente, le "b" l'ajustement pour le moment où y=0. Aux points A et D, tu as un angle, donc tu as une pente. Dans chaque cas, tu as donc le "a", et en utilisant le point par lequel passe la droite, tu récupères le "b".
Tu as donc une droite d1 qui passe par A avec une pente à 50°, et une droite d2 qui passe par D avec une pente à 260°.

Ok, mais tu cherches le point C ? Tu as donc besoin de connaitre l'intersection entre la droite ∆1 perpendiculaire à d1 et qui passe par A, et la droite ∆2 perpendiculaire à d2 et qui passe par D. De mémoire, la pente d'une droite perpendiculaire à une autre, ce serait pas en passant de "a" à "-a" ? (cf éventuellement ailleurs). Donc tu obtiens la pente des perpendiculaires, tu connais un point par lequel elles passent, et (re-)donc tu peux connaitre leur équation.

Tu arrives donc avec l'équation de 2 droites : ∆1 qui passe par A, et ∆2 qui passe par D.
Le point C, c'est l'intersection de ces 2 droites, donc système de 2 équations à 2 inconnues.
Y-a-plus-qu'à.

**BBric** · 01/02/2024, 22h09

J'ai fait mon schéma en vectoriel vite fait, l'angle AB avec la verticale devrait également être de 10°, ce qui n'est pas le cas ici. C'est juste un cas particulier pour illustrer une multitude d'autres cas de figure qui retombent sur un raisonnement similaire mais avec des distances et des radiales différentes. Le point B est plus important que le point D, mais ce dernier représente la fin de l'arc de cercle, j'ai mis toutes les infos des fois que ça puisse servir...

Dans tous les cas je ne connais pas les coordonnées de C et D donc je ne comprends pas votre raisonnement, je peux trouver les équations des droites AB, AC et BD, mais ça ne permet pas de trouver l'intersection en C ou en D. En définissant un point D arbitrairement on peut résoudre le problème mais je préférerais éviter.

Sinon il manque aussi l'angle BAC qui est ici de 30°, et l'angle de l'arc qui est de 210°.
Il n'existe pas une formule de ninja pour résoudre ce genre de problème ? ^^

**Alex64** · 02/02/2024, 10h45

les données de départ sont incohérentes.
cela vient du fait que pour tracer le schéma de BBric les données ont été transférées dans le 4eme quadrant du repère orthonormé.

je pense qu'il faut utiliser ces coordonnées: A(40 ; 114) et B(46 ; 73) ainsi les données sont dans le 1er quadrant.

l'angle en A de 50° est cohérent par contre l'angle de 260 ° en B ne l'est pas! => une angle de 10° ou 190° correspond au schéma

voici mon principe de calcul avec B qui est sur la tangente au cercle au point D

1) je calcule l'intersection T des tangentes suivantes A(40 ; 114) alpha 50° B(46 ; 73) beta 10° => T (-1.419 ; 64.6387)

2) je calcule l'intersection du vecteur normal en A(40 ; 114) alpha =(50°+90°) avec la bissectrice de AB en T => (-1.419 ; 64.6387) bissectrice = (50+10)/2

et cela me donne le centre du cercle C (57,9660 ; 98,9247).