Discussion :

[Invité]

Bonjoir !

Quel rapport avec python ? Peu voire pas du tout, j'avoue...

Dans une image contenant des polygones de 3, 4 ou 5 côtés (triangle équilatéral, carré, octogone équilatéral) à la rotation aléatoire, j'aimerais trouver rapidement le centre de celui sur lequel je clique.

J'ai songé à une méthode (et très certainement réinventé la roue) qui me semble facile à mettre en œuvre en python :



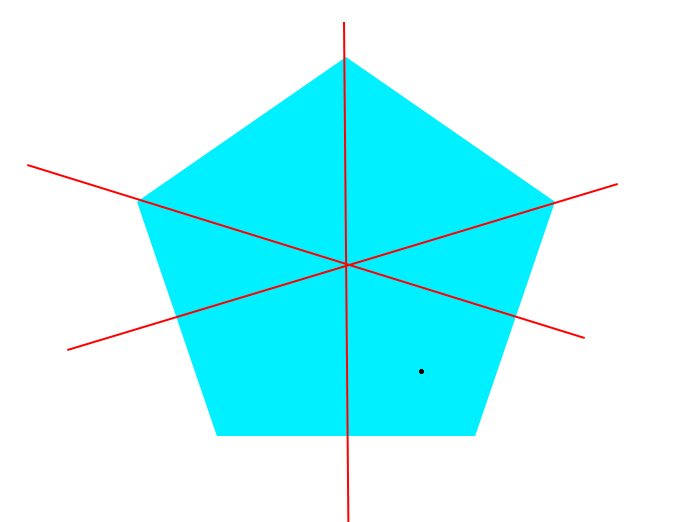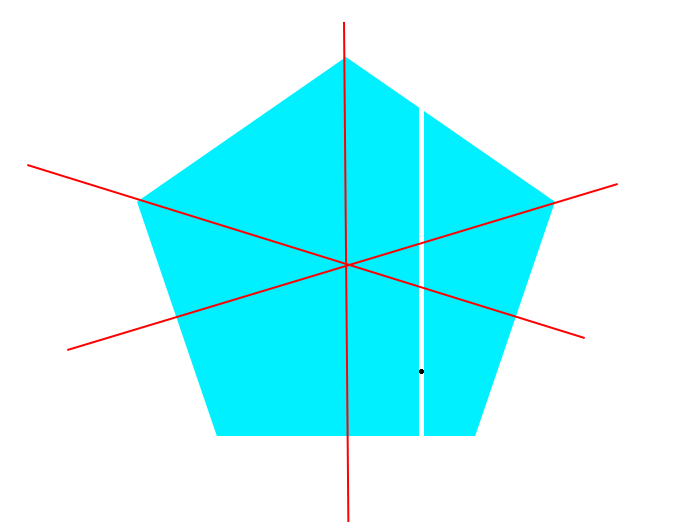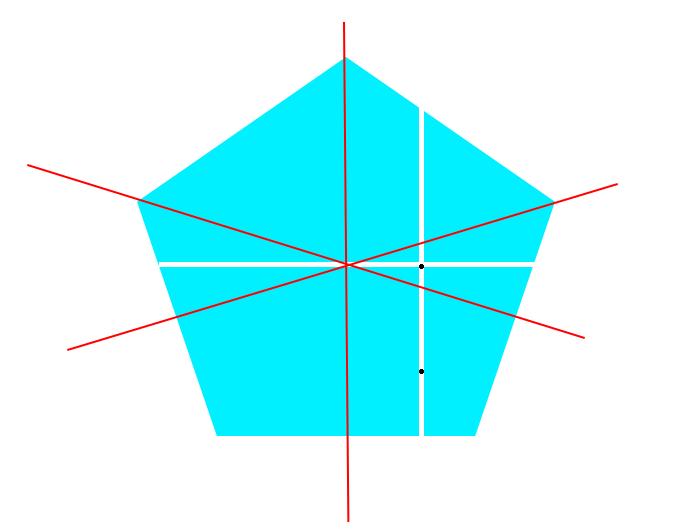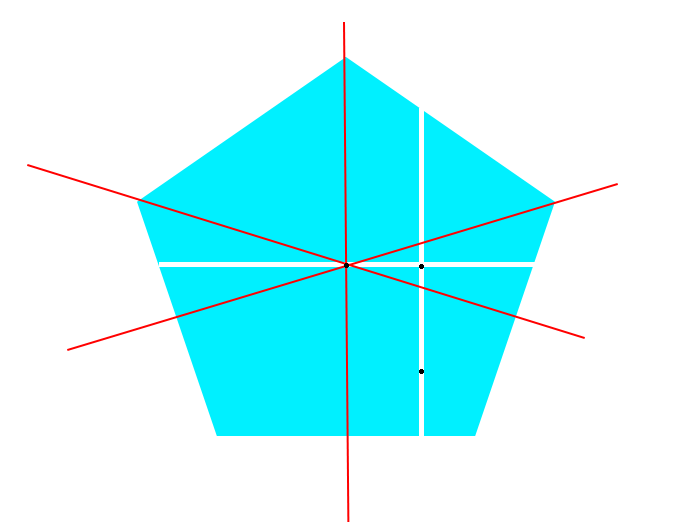
Le premier point noir (en bas du polygone) est l'endroit où j'ai hypothétiquement cliqué, ensuite avec PIL (pix = im.load()) je peux obtenir un tableau 2D des pixels et donc établir ma première droite verticale (while pixel is blue y+1 / idem avec y-1), je peux calculer facilement le centre de cette droite (second point noir) et recommencer à l'horizontale pour déterminer le centre du polygone.

Mon raisonnement vous parait juste ? Y a-t-il plus mieux en terme pythonesque (plus rapide que PIL par ex) ou algorithmique ?

(Vive photoshop)

Merci et bonne joirée !

[Sve@r]

Bonjour

Quel rapport avec python ? Peu voire pas du tout, j'avoue...

Ben oui, ton topic est un topic d'algo...

Dans une image contenant des polygones de 3, 4 ou 5 côtés (triangle équilatéral, carré, octogone équilatéral)

Oui, l'octogone, bâtiment à 5 côtés bien connu abritant le QG du Ministère de la Défense américaine...

ou algorithmique ?

Pour les octogones impairs ce serait le point d'intersection des médianes (et 2 suffisent) et pour les octogones pairs le point d'intersection des diagonales. Reste les octogones à 1 côté...

[Invité]

Ben oui, ton topic est un topic d'algo...

Oui je sais. C'est un petit entracte !

Pour les octogones impairs ce serait le point d'intersection des médianes (et 2 suffisent) et pour les octogones pairs le point d'intersection des diagonales...

C'est surement pas facile ni rapide à calculer depuis une image... Faudrait que je me fasse quelques croquis avec des rotations différentes pour voir si ma proposition tiens la route.


Vive la république ! Vive l'octogone !

[umfred]

je croyais qu'un octogone avait toujours 8 côtés (étymologiquement 8 angles, donc 8 sommets) donc un nombre pair de côtés

[Sve@r]

je croyais qu'un octogone avait toujours 8 côtés (étymologiquement 8 angles, donc 8 sommets) donc un nombre pair de côtés

C'était une moquerie sur le premier post, où le PO cites des figures à 3, 4 et 5 côtés qu'il nomme respectivement triangle, carré et octogone...

[umfred]

j'ai pas bien tilté sur le comique de répétition

[Mat.M]

je peux obtenir un tableau 2D des pixels et donc établir ma première droite verticale (while pixel is blue y+1 / idem avec y-1

oui je pense qu'il faut partir sur cette méthode là.
La méthode serait la suivante:
*parcourir chaque point de l'écran ligne par ligne afin de définir les sommets x,y des polygones en testant si chaque pixel PixelX,PixelY est bleu : une ligne d'écran c'est la largeur de l'image mettons 640 pixels.
Le premier sommet sera donc la première ligne horizontale ne comprenant qu'un seul point bleu
*les sommets suivants seront la ligne comprenant le plus de points bleus
*le sommet le plus bas sera la dernière ligne ne comprenant qu'un seul point
*ranger ces sommets dans un tableau.
*avec ces points définir les droites /vecteurs entre ces points.
*en obtenant ces points on peut avoir le milieu de ces droites.


Sinon la méthode la plus simple c'est de définir les sommets du polygone.
En obtenant les sommets du polygone trouver l'équation du cercle passant par ces sommets.
Au boulot

[Sve@r]

Sinon la méthode la plus simple c'est de définir les sommets du polygone.
En obtenant les sommets du polygone trouver l'équation du cercle passant par ces sommets.

Euh... pour trouver l'équation d'un cercle, équation de type (x-xC)²+(y-yC)²=r² (avec xC et yC les coordonnées du centre C), n'est-il pas nécessaire de connaitre au préalable le centre du cercle (donc ici le centre du polygone)?
Donc en résumé, la méthode la plus simple pour trouver le centre du polygone c'est d'avoir le centre du polygone. Ca se tient...

[wiztricks]

Donc en résumé, la méthode la plus simple pour trouver le centre du polygone c'est d'avoir le centre du polygone. Ca se tient...

Pour les polygones réguliers (convexe)s l'intersection des médianes de 2 côtés donnera le centre du cercle inscrit.
Et pour avoir ces côtés, il faut avoir les coordonnées des points qui en sont les sommets.

Et si on prend le problème de départ, si à partir de la médiane d'un côté on récupère le segment qui va du milieu du coté au point opposé du cercle inscrit.
Si le milieu de ce segment était le centre de ce cercle, le cote serait de longueur nulle (et le prétendu polygone: un cercle).

- W

[Invité]

Euh vous êtes gentils mais c'est un truc prise de tête que vous me proposez là les pros !

Je rajoute à mon énoncé que le centre peut être approximatif.

Ma proposition n'est malheureusement pas aussi précise que je l'espérais mais ça n'est pas trop éloigné de la réalité :

Vive Geogebra !

[wiztricks]

Ma proposition n'est malheureusement pas aussi précise que je l'espérais mais ça n'est pas trop éloigné de la réalité

Reste à calculer les erreurs de cette méthode pour voir si sa précision est intéressante (et dans quels cas).

Euh vous êtes gentils mais c'est un truc prise de tête que vous me proposez là les pros !

ah ben... mais si vous voulez de l'aide on a déjà mentionné que ce n'était pas (ici) le bon forum.

- W