Discussion :

[AbsoluteLogic]

Bonjour,

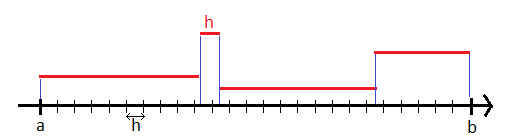
Pour un segment [a,b], j'ai une subdivision donnée de taille N: le segment est divisé en N sous-segments disjoints dont la réunion fait [a,b].
Etant donnée une valeur x, je souhaiterais savoir à quel intervalle de la subdivision il appartient, si possible en temps constant.
J'ai fait quelques recherches, et j'ai trouvé ce sujet. Mais la meilleure solution reste en O(log(N)) au pire.

Cependant, je suis intrigué sur le fait que ce ne soit pas possible de le faire en temps constant pour deux raisons :
- on peut imaginer une discrétisation du segment, qui transforme alors ce dernier en tableau dans lequel chaque élément correspond à l'indice du sous intervalle correspondant. On a alors une complexité constante: il faut juste lire la valeur dans le tableau. Evidemment, on ne peut pas se permettre de discrétiser le segment, mais je me dit (sûrement à tort) que ce qui est faisable en discret peut être faisable en continu...
- le problème me fait penser aux tables de hachage (que je ne connais pas très bien), qui à une valeur en associe une autre en temps constant. N'y aurait-il pas moyen de ramener nos sous-intervalles à ces valeurs?

De plus, je peux me permettre de faire un travail préliminaire (connaissant la subdivision mais pas la valeur x) qui n'a pas besoin d'être en temps constant.

Voilà, si vous connaissez des méthodes dans ce domaine, ou que vous avez des idées sur le sujet, je suis preneur.
Merci d'avance

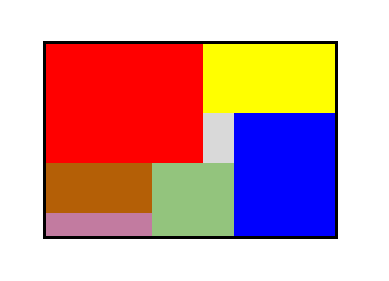
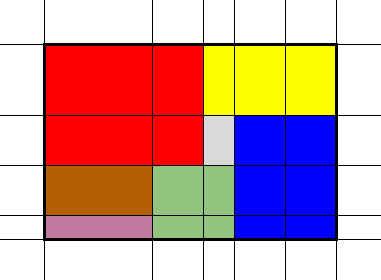
PS: mon problème est en fait en deux dimensions: un rectangle divisé en sous-rectangles, mais je pose d'abord le problème en une dimension, en espérant ensuite pouvoir le ramener en 2D (voire n dimensions )

[anapurna]

salut

en prenant la valeur median de ton segment et faire une recherche dichotomique cela ne le ferais pas ?
il Faut chercher la valeur la plus proche et normalement tu trouve le bon segment
pour la 2d il faudra prendre le point median en x et en y et appliquer la meme regle sur les rectangle cela devrais te limiter ta recherche
ce qui te donne une complexité de ... O(logn) je ne pense pas que tu pourra pas faire mieux

[AbsoluteLogic]

en prenant la valeur median de ton segment et faire une recherche dichotomique cela ne le ferais pas ?
[...]
une complexité de ... O(logn) je ne pense pas que tu pourra pas faire mieux

Salut. Merci d'avoir porté ton intérêt au problème.
Oui, la dichotomie est une solution pour obtenir du log(N), comme il l'a été évoqué dans le sujet que j'ai indiqué.
Mais j'ai toujours espoir qu'il y ait une solution en temps constante (éventuellement avec un travail préliminaire non constant) dans la mesure où j'ai évoqué deux problèmes proches résolubles en temps constant...

[pseudocode]

le problème me fait penser aux tables de hachage (que je ne connais pas très bien), qui à une valeur en associe une autre en temps constant.

C'est en temps constant seulement si on fixe un certains nombres de paramètres, en particulier le nombre de bits et d'opérations par bit.

De même, ta recherche dichotomique en o(log(n)) sera "en temps constant" si tu fixes le nombre de subdivisions N.

[Flodelarab]

Bonjour

L'équivalent continu d'un tableau (associatif ou non) s'appelle une fonction.
En l'occurrence, ici, c'est une fonction en escalier.

Charge pour toi de trouver la meilleure façon de définir.

Je pense en particulier à la fonction sigmoïde utilisée dans les réseau de neurones, que tu peux utiliser comme une fonction de heaviside que tu empilerais.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

gnuplot> plot [0:10][0:10] 0, 2/(1+exp(100*(-x)))+ 5/(1+exp(100*(5-x))) - 3/(1+exp(100*(8-x)))

[disedorgue]

Déjà, comment représentes-tu ton rectangle initial par rapport aux sous rectangles ?
Ont-ils une largeur et longueur différente ou seulement soit la longueur soit la largeur ?

Comment représentes-tu X dans le plan ?

[AbsoluteLogic]

Merci à tous pour avoir pris le temps de me répondre

C'est en temps constant seulement si on fixe un certains nombres de paramètres, en particulier le nombre de bits et d'opérations par bit.

De même, ta recherche dichotomique en o(log(n)) sera "en temps constant" si tu fixes le nombre de subdivisions N.

Certes, j'imagine que tu veux mettre en avant qu'il y a une infinité d'intervalle possibles, alors qu'un dictionnaire prend un nombre fini d'entiers possibles en entrée.
Mouais, je ne suis pas convaincu, en allant par là, même le nombre d'intervalle possibles est fini puisque leurs extrémités sont codées sur un certain nombre de bit...

Bonjour

L'équivalent continu d'un tableau (associatif ou non) s'appelle une fonction.
En l'occurrence, ici, c'est une fonction en escalier.

Charge pour toi de trouver la meilleure façon de définir.

Je pense en particulier à la fonction sigmoïde utilisée dans les réseau de neurones, que tu peux utiliser comme une fonction de heaviside que tu empilerais.

Houlà, ça fait drôle d'entendre parler des réseaux de neurones et des fonctions sigmoïde, alors que c'est justement ce que je suis en train d'étudier à mon école! Mais en aucun j'en aurai parlé sur ce sujet ^^
C'est vrai, l'idée serait tout simplement d'évaluer une certaine fonction en escalier. Mais je ne pense pas qu'une fonction de Heaviside soit une solution, puisque si l'on considère la complexité par rapport à l'opération la plus longue - ici l'exp -, on reste en temps linéaire par rapport au nombre d'intervalle.
Je fais alors le raisonnement suivant:
Pour évaluer la fonction en escalier en temps constant, il faudrait le représenter par son graphe. Mais cela implique de le discrétiser puisqu'on est en informatique . On pourrait donc se dire que ça ne sert à rien: on a justement pris une fonction pour rendre le problème continu, qu'est-ce qu'il raconte là?
En fait, ça me donne une idée: si on prend comme pas de discrétisation la longueur du plus petit intervalle de notre liste, on peut représenter la subdivision par un tableau dont chaque élément correspond à un pas, et contient le triplet (intervalle de gauche, abscisse de changement, intervalle de droite) si il y a un changement d'ordonnée sur ce pas. Et puisque le pas correspond à la longueur du plus petit intervalle, alors il ne pourra pas y avoir deux changements d'intervalle sur le même pas.

Du coup, cela répond à mon problème: on pourra, avec x donné, récupérer l'intervalle correspondant en allant chercher dans le tableau l'élément correspondant et en faisant une comparaison de x avec "l'abscisse de changement". Cela se fait en temps constant, avec une préparation d'un coût non constant. Mais le problème, c'est que l'on est même pas en mesure de connaître ce coût de préparation (et la mémoire occupée) en fonction du nombre d'intervalle, puisque ce sera en O((b-a)/(longueur minimale)).
Mais bon, si la complexité de la préparation n'a pas besoin d'être majorée, ça va. Et libre à nous de trouver un compromis en permettant par exemple de pouvoir encoder 2 (ou plus) changements de valeur sur un pas au lieu d'un seul.
Voilà, je marque le sujet en résolu. Mais il n'est pas interdit de proposer des solutions encore plus performantes, à la fois en terme de mémoire consommée ou de complexité de préparation.

Déjà, comment représentes-tu ton rectangle initial par rapport aux sous rectangles ?
Ont-ils une largeur et longueur différente ou seulement soit la longueur soit la largeur ?

Comment représentes-tu X dans le plan ?

C'est juste un ensemble de rectangles qui en "pave" un plus gros comme sur la figure suivante:

Et je peux facilement me ramener à un problème en une dimension, en me ramenant à un quadrillage séparant tous ces rectangles, en en étudiant séparément les abscisses et les ordonnées:

[disedorgue]

Et si j'ai bien compris, X est un point et le but est de savoir dans quel rectangle il se trouve ?

Et dans un espace à 3 dimensions, l'algo doit aussi fonctionner ?

Je pose cette question, car pour le cas du plan rectangulaire, intuitivement, je pense que c'est possible de passer par des vecteurs, mais comme je dis, pour l'instant c'est juste intuitif, donc pas encore sur de moi...