Discussion :

[Basile le disciple]

slt à tous,

je bloque depuis plusieurs jours sur un exercice. Mon algorithme marche mais met trop de temps

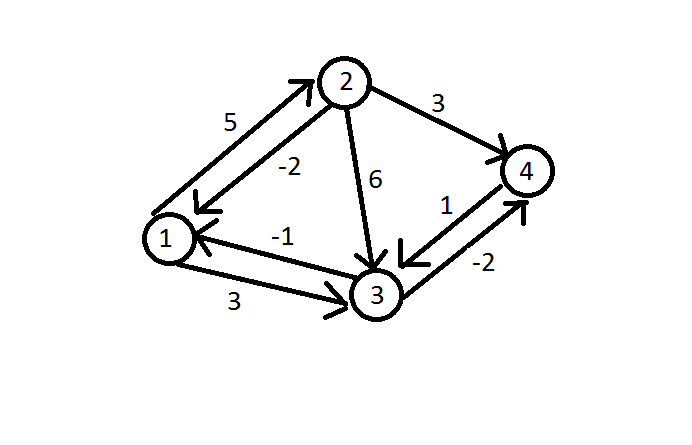
je dispose d'un labyrinthe sous la forme d'un graphe pondéré orienté et je dois trouver, à partir d'un sommet déterminé, le chemin le plus bénéfique(maximum de points récoltés) en visitant un nombre déterminé de chemin... un exemple :



je dois partir au sommet n°1 et amasser les points en traversant 4 chemins (je peux aussi attendre à un sommet et récolté 0 points si c plus avantageux). La solution ici serait 15 avec le chemin 1-2 2-3 3-1 1-2

voilà ce que l'on me donne en entrée :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
 
4 8 1 4
1 2 5
1 3 3
2 1 -2
2 3 6
2 4 3
3 1 -1
3 4 -2
4 3 1

les 4 premiers nombres sont respectivement :

nbSommets : nombre de sommets
nbArcs : nombre d'arcs
debut : sommet de départ
temps : temps à disposition

les nbArcs lignes suivantes (sous la forme s1 s2 l) décrivent le graphe (s1 relie s2 avec un poid l)

et voici mes algos (en python):

une version récursive :

Code python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
 
import sys
 
def main():
  nbSommets,nbArcs,debut,temps = map(int,sys.stdin.readline().split())
  INFINI = 10**8
  #INFINI = 100  #<-- à supprimer
  voisin = [ [(i,0)] for i in range(nbSommets+1)]
  for _ in range(nbArcs):
    s1,s2,poid = map(int,sys.stdin.readline().split())
    voisin[s1].append( (s2,poid) )
 
  tabDynamique = [ [INFINI for i in range(temps)] for j in range(nbSommets+1)]
 
  def MeilleurChemin(T,s):
    if T ==0:
      return 0
    if tabDynamique[s][T-1] != INFINI:
      return tabDynamique[s][T-1]
 
    maxPoint = 0
    for v,bonus in voisin[s]:
      maxPoint = max(maxPoint,bonus + MeilleurChemin(T-1,v) )
 
    tabDynamique[s][T-1] = maxPoint
    return maxPoint
 
  print(MeilleurChemin(temps,debut))
 
 
 
main()

une version itérative :

Code python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
 
import sys
 
def main():
  nbSommets,nbArcs,debut,temps = map(int,sys.stdin.readline().split())
  INFINI = 10**8
  #INFINI = 100  #<-- à supprimer
  voisin = [ [(i,0)] for i in range(nbSommets+1)]
  visites = [False] * (nbSommets+1)
  visites[debut] = True
  scoresMax = [ [-INFINI for _ in range(temps+1)] for i in range(nbSommets+1)]
  scoresMax[debut][0] = 0
  scoreMax = -INFINI
  for _ in range(nbArcs):
    s1,s2,poid = map(int,sys.stdin.readline().split())
    voisin[s1].append( (s2,poid) )
 
  en_cours = [debut]
 
  for t in range(1,temps+1):
    for i in range(len(en_cours)):
      s = en_cours[i]
      for v,p in voisin[s]:
        #print(v,p)
        scoresMax[v][t] = max(scoresMax[v][t],scoresMax[s][t-1] + p)
        scoreMax = max(scoreMax,scoresMax[v][t])
        if not visites[v]:
          visites[v] = True
          en_cours.append(v)
 
  sys.stdout.write(str(scoreMax))
 
main()

mon problème est donc qu'ils prennent trop de temps et je poste pr savoir si qqn n'aurait pas une idée pr améliorer... Merci d'avance