Bonjour,
Je cherche à savoir si un calcul que je fais est invariant par translation...
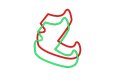
Explications : prenons un contour fermé, qu'on nomme A, quelconque. Appliquons lui une transformation, quelconque (pour le moment), ce qui nous donne le contour B.
Par exemple dans le cas d'une translation :
Je connais tous les vecteurs qui lient les points de A aux points de B (cad les points image de A par la transformation appliquée).
Voici mon calcul : je somme les valeurs scalaires des vecteurs ( un vecteur est positif s'il est orienté vers l'intérieur de A, négatif sinon).
En version analytique, la somme que je fais des vecteurs est
où m est le vecteur de déplacement à l'abscisse curviligne s, N est le vecteur normal (toujours orienté vers l'intérieur du contour).
En gros cela peut s'apparenter au calcul approximatif du mouvement global de mon contour.
Question : est-ce que cela donne 0 si ma transformation est une translation ?
cad, si pour tout s, m(s) = t, où t est constant, est-ce que cette intégrale est nulle ?
J'aurais tendance à dire que non à cause de m... Mais je vois pas comment le prouver...
Bon je sais pas si ce que j'ai demandé est clair, mais je sais qu'ici il ya plein de supers matheux qui peut-être auront la solution...
Merci,
Mathieu.











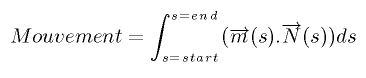
 Répondre avec citation
Répondre avec citation










Partager