Discussion :

[SpiceGuid]

Je ne permets de commencer par un peu d'auto-promotion en vous présentant mon projet ERic.
ERic est un éditeur de graphes conceptuels équipé d'un algorithme de subsomption.
À la base de cet algorithme de subsomption il y a un algorithme efficace de H-coloration.

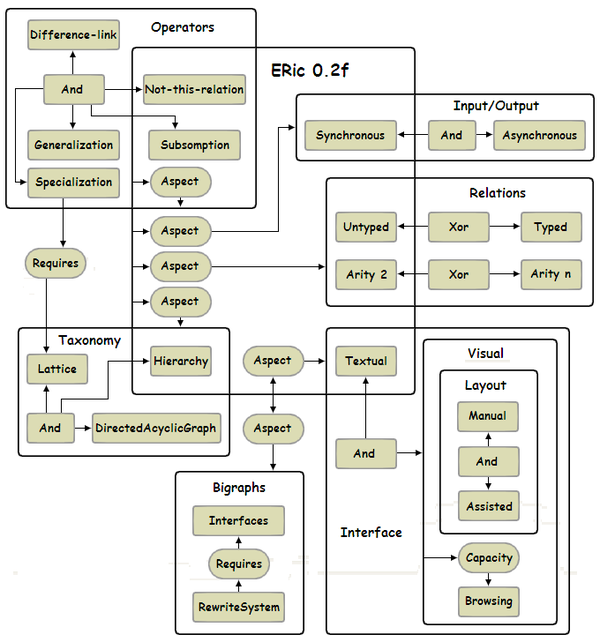
Voici le document qui me sert à planifier le développement :

• Une boîte And signifie que dans le futur pourrait ERic potentiellement offrir toutes les options.
  
• Une boîte Xor signifie que les options sont mutuellement exclusives.

Pour le futur proche j'ai décidé que la prochaine mise-à-jour de ERic 0.2f à ERic 0.2g offrira les Difference-link.
Graphiquement cela signifie que la boîte Difference-link en haut à gauche restera dans la boîte Operators tout en rentrant dans la boîte ERic 0.2g, comme c'est déjà le cas pour la boîte Difference-link.

Ajouter de telles extensions n'est pas trivial pour moi.
C'est pourquoi j'ai décidé d'améliorer mon niveau en Coq afin de mieux maîtriser l'algorithme de base.

Comme je suis débutant je vais commencer par des choses simples

[SpiceGuid]

À la base du problème de la H-coloration il y a la subsomption.

J'ai deux hiérarchies :

• Une hiérarchie pour les concepts.
• Une hiérarchie pour les relations.

En interne une hiérarchie est représentée par un arbre binaire :

• L'horizontale à droite désigne un frère.
• La verticale en bas désigne la fratrie d'enfants.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
  A
  |
  B-----------------C-----D
  |                 |     |      
  E------F------G   H     I------J

• A possède 3 enfants : B, C et D
• B possède 3 enfants : E, F et G
• C possède 1 enfant : H
• D possède 2 enfants : I et J

L'opération de base consiste à demander si un nœud est ou non le descendant d'un autre. Cependant comme une hiérarchie de concepts (ou de relations) est potentiellement très profonde (beaucoup plus qu'une hiérarchie de classes en POO) la méthode consistant à remonter d'un nœud vers la racine est trop lente.

D'où une méthode alternative consistant à labelliser les nœuds avec un intervalle entier.
Un nœud est le descendant d'un autre ⇔ son intervalle est inclus dans celui de l'autre.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
[0,10]
  |
[1,5]-------------[5,7]-[7,10]
  |                 |     |      
[2,3]-[3,4]-[4,5] [6,7] [8,9]-[9,10]

Traduction en OCaml :

Code OCaml 3.12.1 :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
type 'a node =
   | Empty
   | Node of 'a * 'a node * 'a node

type interval =
   | Interval of int * int

let rec compress_ancestry n acc =
   match n with
   | Empty -> Empty,acc
   | Node((),alt,sub) ->
         let s,r = compress_ancestry sub (succ acc) in
         let a,m = compress_ancestry alt r in
         Node(Interval(acc,r),a,s),m

Petit test pour vérifier que compress_ancestry se comporte comme sur le schéma :

Code OCaml 3.12.1 :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
let a =
   let e = Node((),Node((),Node((),Empty,Empty),Empty),Empty) in
   let h = Node((),Empty,Empty) in
   let i = Node((),Node((),Empty,Empty),Empty) in
   let b = Node((),Node((),Node((),Empty,i),h),e) in
   Node((),Empty,b)
in compress_ancestry a 0

Traduction en Coq :

Code Coq 8.3 :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Inductive node (A : Type) : Type :=
| Empty : node A
| Node : A -> node A -> node A -> node A.
   
Inductive interval : Type :=
| Interval : nat -> nat -> interval.

Fixpoint compress_ancestry n acc :=
   match n with
   | Empty => (Empty interval,acc)
   | Node tt alt sub =>
         let (s,r) := compress_ancestry sub (S acc) in
         let (a,m) := compress_ancestry alt r in
         (Node interval (Interval acc r) a s,m)
   end.

Je suis très tenté par ce type interval :

Code Coq 8.3 :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
Inductive interval : Type :=
| Interval : forall min max, min < max -> interval.

Check Interval 0 9 (lt_0_Sn 8).
Check Interval 1 2 (lt_n_Sn 1).

Fact lt_1_9 : 1 < 9. Proof. repeat constructor. Qed.
Check Interval 1 9 lt_1_9.

Mais je ne comprends pas comment je pourrais l'intégrer dans compress_ancestry.

[SpiceGuid]

Énoncé du théorème principal qui dit que l'appartenance d'un nœud à une hiérarchie est équivalent à l'inclusion d'un intervalle dans un autre.

Code Coq 8.3 :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Inductive node {A : Type} : Type :=
| Empty : node
| Node : A -> node -> node -> node.
   
Inductive interval : Type :=
| Interval : nat -> nat -> interval.

Fixpoint compress_hierarchy n acc :=
   match n with
   | Empty => (Empty,acc)
   | Node tt alt sub =>
         let (s,r) := compress_hierarchy sub (S acc) in
         let (a,m) := compress_hierarchy alt r in
         (Node  (Interval acc r) a s,m)
   end.

Inductive sibling {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| equal_sibling : forall n, sibling n n
| alt_sibling : forall a alt sub, sibling (Node a alt sub) alt.
   
Inductive member {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| equal_member : forall a alt sub, member (Node a alt sub) (Node a alt sub)
| sibling_member : forall a alt alt1 alt2, sibling alt1 alt2 -> member (Node a alt alt1) alt2. 

Inductive includes : node (A:=interval) -> node (A:=interval)-> Prop :=
| node_includes : 
   forall la ra alta suba lb rb altb subb,
   la <= lb /\ rb <= ra -> includes
   (Node (Interval la ra) alta suba)
   (Node (Interval lb rb) altb subb).
   
Theorem member_iff_includes :
   forall n a b,
   let (h,_) := compress_hierarchy n O in 
   member h a -> member h b ->
   member a b <-> includes a b. 
Admitted.

Prochaine étape : énoncer le théorème qui dit que compress_hierarchy préserve la hiérarchie.

[dividee]

Bonjour SpiceGuid,

Tes définitions de sibling et member me semblent bizarres; elles ne sont même pas récursives, et puis sibling devrait sans doute être symétrique (ou alors il faudrait l'appeler autrement).

J'aurais plutôt écris qqch comme ça:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
Inductive sibling {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| equal_sibling : forall n, sibling n n
| alt_sibling   : forall a alt n sub, sibling alt n -> sibling (Node a alt sub) n
| sym_sibling   : forall n m, sibling n m -> sibling m n.

Inductive member {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| equal_member   : forall n, member n n
| sibling_member : forall a alt sub1 sub2 n,
                   member sub2 n -> sibling sub1 sub2 -> member (Node a alt sub1) n.

ou bien en utilisant le module Relations:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
Require Import Relations.

Inductive sibling_step {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| alt_sibling : forall a alt sub, sibling_step (Node a alt sub) alt.

Definition sibling {A : Type} := clos_refl_sym_trans node (sibling_step (A:=A)).

Inductive member_step {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| sibling_member : forall a alt alt1 alt2, sibling alt1 alt2 -> member_step (Node a alt alt1) alt2.

Definition member {A : Type} := clos_refl_trans node (member_step (A:=A)).

[dividee]

Oops, il vaudrait sans doute mieux éviter d'avoir forall n, sibling n Empty et forall n, member n Empty:

Donc plutôt ceci:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
Inductive sibling {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| equal_sibling : forall a alt sub, sibling (Node a alt sub) (Node a alt sub)
| alt_sibling   : forall a alt sub n, sibling alt n -> sibling (Node a alt sub) n
| sym_sibling   : forall n m, sibling n m -> sibling m n.

Inductive member {A : Type} : node (A:=A) -> node (A:=A) -> Prop :=
| equal_member   : forall a alt sub, member (Node a alt sub) (Node a alt sub)
| sibling_member : forall a alt sub1 sub2 n,
                   member sub2 n -> sibling sub1 sub2 -> member (Node a alt sub1) n.

[SpiceGuid]

Pour sibling je vais chercher un autre nom parce que je ne vois pas l'intérêt de la symétrie.

Utiliser le module Relations j'imagine que ça pourrait éventuellement m'éviter d'avoir à réinventer la roue.