Une implémentation Java de l'algorithme Expectation-maximization (EM).
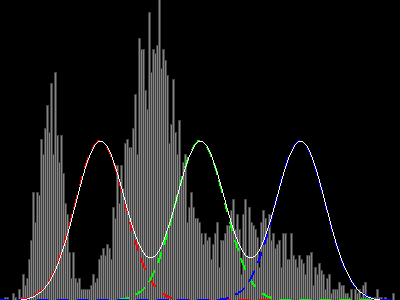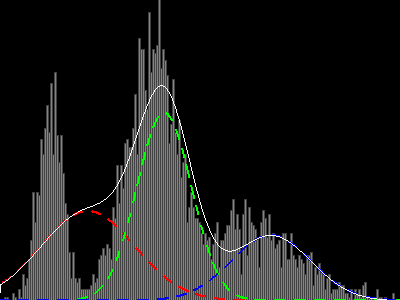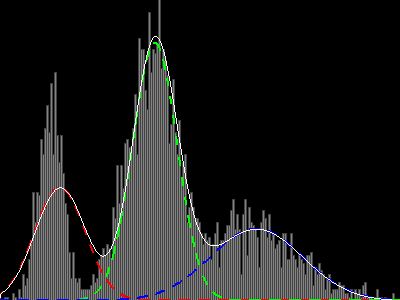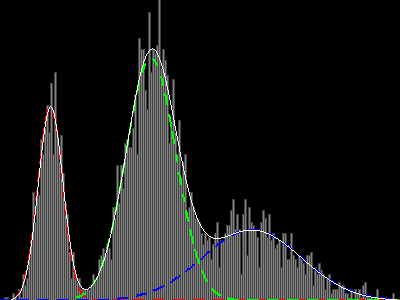
exemple de convergence avec 3 distributions normales (voir post suivant)
L'interface qui définit une loi de probabilité
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Le code de l'algorithme EM
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54















 Répondre avec citation
Répondre avec citation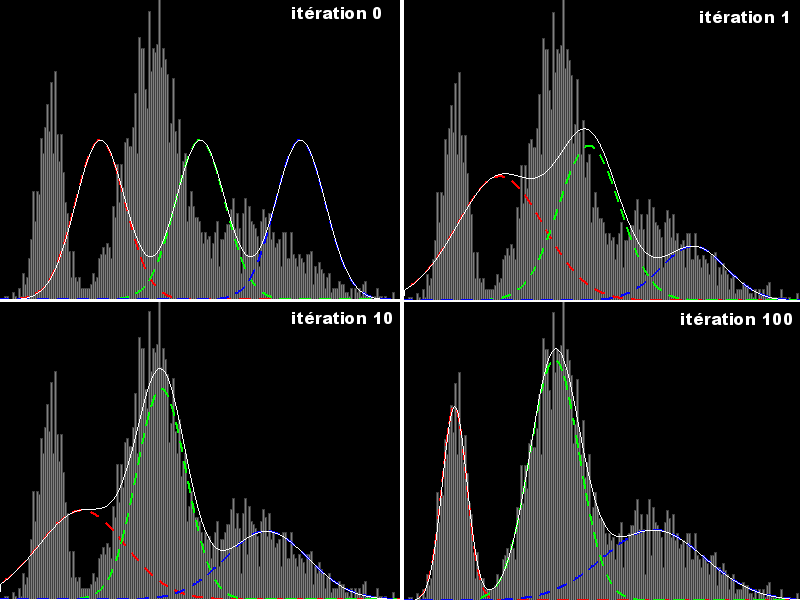



Partager