Le code suivant est une implémentation Java des formules du document

Projective Mappings for Image Warping (1989) by Paul Heckbert

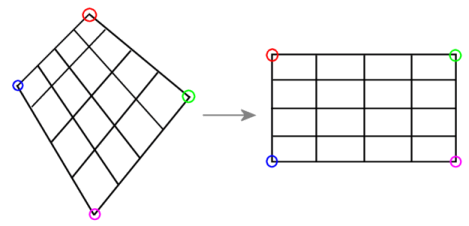
Cette implémentation simple permet de transformer une zone quadrilatère quelconque en une zone rectangulaire.



Le programme principal:
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
 
public static void main(String[] args) {
	Image source = new Image("yourimage.jpg");
 
	// 4 points qui définissent un quadrilatère convexe
	Point P1 = new Point(10,71);
	Point P2 = new Point(134,71);
	Point P3 = new Point(71,24);
	Point P4 = new Point(62,24);
 
	// résolution du système linéaire
	double[] system = getSystem(P1,P2,P3,P4);
	System.out.println(Arrays.toString(system));
 
	// création de l'image corrigée
	int W=640,H=480;
	Image target = new Image(W,H);
 
	// pour chaque pixel (x,y) de l'image corrigée
	for(int y=0;y<H;y++) {
		for(int x=0;x<W;x++) {
 
			// conversion dans le repère orthonormé (u,v) [0,1]x[0,1]
			double u = (double)x/W;
			double v = (double)y/H;
 
			// passage dans le repère perspective
			double[] P = invert(u, v, system);
 
			// copie du pixel (px,py) correspondant de l'image source 
			// TODO: faire une interpolation pour avoir de meilleurs résultats
			int px=(int)Math.round(P[0]);
			int py=(int)Math.round(P[1]);
			target.setrgb(x, y, source.getrgb(px, py) );
		}
	}
}

Et les algos de calcul issus du document dont j'ai donné le lien ci-avant
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
 
public static double[] getSystem(Point... P) {
	double[] system = new double[8];
	double sx = (P[0].x-P[1].x)+(P[2].x-P[3].x);
	double sy = (P[0].y-P[1].y)+(P[2].y-P[3].y);
	double dx1 = P[1].x-P[2].x;
	double dx2 = P[3].x-P[2].x;
	double dy1 = P[1].y-P[2].y;
	double dy2 = P[3].y-P[2].y;
 
	double z = (dx1*dy2)-(dy1*dx2);
	double g = ((sx*dy2)-(sy*dx2))/z;
	double h = ((sy*dx1)-(sx*dy1))/z;
 
	system[0]=P[1].x-P[0].x+g*P[1].x;
	system[1]=P[3].x-P[0].x+h*P[3].x;
	system[2]=P[0].x;
	system[3]=P[1].y-P[0].y+g*P[1].y;
	system[4]=P[3].y-P[0].y+h*P[3].y;
	system[5]=P[0].y;
	system[6]=g;
	system[7]=h;
 
	return system;
}
 
public static double[] invert(double u, double v, double[] system) {
	double x = (system[0]*u+system[1]*v+system[2])/(system[6]*u+system[7]*v+1); 
	double y = (system[3]*u+system[4]*v+system[5])/(system[6]*u+system[7]*v+1);
	return new double[]{x,y};
}