Bonjour,
je ne suis pas sûr que je suis dans la bonne section, mais je ne sais pas où poster (algorithme peut-être ? )
Je cherche à approximer une probabilité dépendant d'une loi binomiale avec cette formule :
(source Wikipedia)
Le problème, c'est que j'obtiens très vite des overflow avec mon calcul de factorielle énorme (j'ai un n entre 200 et 250)
Comment faire pour approximer cela ?












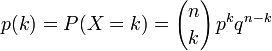
 Répondre avec citation
Répondre avec citation









Partager