Discussion :

[titpuce]

Bonjour,
Je vous soumet un petit problème (j'ai une partie de la solution, mais je pense qu'il y a beaucoup moins couteux et plus élégant).
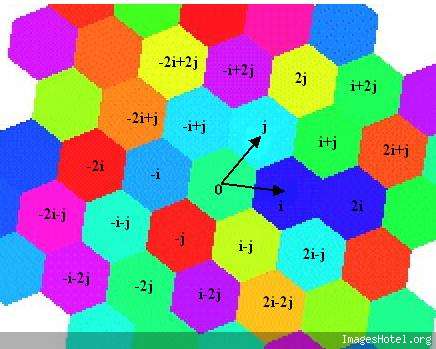
J'ai un assemblage rectangulaire dans lequel je vais mettre des mailles. l'ensemble de ces mailles va former un hexagone, dans lequel j'aimerai pouvoir gérer des symétries.

en dessin cela donne : chaque - représente une case vide.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
°° 1234567
01 ---f---
02 --f-f--
03 -f-f-f-
04 f-f-f-f
05 -f-f-f-
06 f-f-f-f
07 -f-f-f-
08 f-f-f-f
09 -f-f-f-
10 f-f-f-f
11 -f-f-f-
12 --f-f--
13 ---f---

La structure est réalisée avec des cases rectangulaires, ce qui lui donne un aspect moin "aplati" que sur mon dessin, mais bref, passons.
Dans cette structure, il y a des cases équivalentes.
Si je découpe l'hexagone formé en six, je vais avoir six cadrans symétriques. Par conséquent, il y a des cases équivalentes : si l'on s'aide des coordonnées de ligne/colonne de chaque case (chaque lettre dans mon schéma), cela donne : la case (13;4) est équivalente par symétrie médiane à la case (1;4).
Si je prend un secteur de cet hexagone de 60° et que, pour la pointe de ce secteur (case (13;4)), je cherche toutes les cases équivalentes, je vais trouver : (1;10), (1;4) (4;1) (7;4) (7;10).

La question du jour : trouver un algorithme simple qui me donne, connaissant la composition d'un secteur de 60° la composition de tout l'hexagone obtenue après rotation de ce secteur.
Dans l'exemple que j'ai donné toutes les cases sont identiques, mais dans la réalité ce n'est pas toujours le cas.
Faire la même chose pour tous les types de symétries possibles dans un hexagone, et toutes les rotations.

[titpuce]

je fais remonter, ça n'a pas l'air d'inspirer grand monde...
J'ai vu qu'il y avait des codes pour gérer les structures hexagonales, mais en s'aidant du voisin. A priori je ne peux pas les utiliser dans ce cas là, sauf si qq'un me prouve le contraire, ce qui m'arrangerait bien

[Nemerle]

je fais remonter, ça n'a pas l'air d'inspirer grand monde...

faudrait que tu expliques mieux en particulier "Si je prend un secteur de cet hexagone de 60° et que, pour la pointe de ce secteur (case (13;4)), je cherche toutes les cases équivalentes, je vais trouver : (1;10), (1;4) (4;1) (7;4) (7;10)."

En particulier, je dirais la même chose qu'à Charly: cherche "système radiciel" --> il existe une "base" (u,v) qui te permet de placer tes hexagones et de travailler simplement avec tes rotations.

Ensuite, il te suffit de passer de ta base (u,v) à ta base standard (x,y).

[Nemerle]

Considère la base (i,j) suivante:



- le centre est un centre d'un hexagone choisi par toi
- i est le vecteur qui relie ce centre au centre de l'hexagone voisin "de droite"
- j est le vecteur qui relie ce centre au centre de l'hexagone voisin "en haut à droite" (l'angle (i,j) est donc de 60 degrés)

Dans cette base, tous les centres des hexagones s'écrivent ai+bj ou i,j sont des entiers relatifs. Par exemple, en partant du centre

....j-i.....j
-i......0.....i
....-j....i-j

Travailler avec des rotations est alors plus simple dans cette base (=réseau radiciel associé à notre hexagone)

[titpuce]

merci Nemerle
Zai toujours pas compris ce qu'était un système radiciel, mais je suppose que c'est un autre référentiel de base... Google n'est pas très causant dessus....

Si je comprends bien ton explication, je dois dans mon algo travailler d'abord en ne considérant que les hexagones.
Mais si j'ai trois couronnes d'hexagones autour de ma cellule centrale, comment calculer les coordonnées selon ton système ?
Si je veux les coordonnées des trois cellules situées sous la cellule centrale je calcule :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
0
i-j
i-2j
2i-3j

Est-ce exact ?

[Nemerle]

Mais si j'ai trois couronnes d'hexagones autour de ma cellule centrale, comment calculer les coordonnées selon ton système