Bonjour à tous,
Afin de réaliser quelques tests géométriques en 2D, je cherche un moyen de pouvoir insérer un sommet A à la liste des sommets S définissant le polygone P, initialement tracé dans un ordre unique et particulier (12345...), tel que le nouveau polygone P', alors défini par une liste de sommets S':=(S inclu A), respecte les quelques règles simples ci-dessous :
- le polygone initial et ou final peut être convexe ou concave mais non croisé
- le polygone final est tracé dans le même ordre que le polygone initial
- la liste des sommets initiale n'est modifiée que par l'insertion d'un nouveau sommet ; l'ordre n'est pas modifié (ex : {1,2,3,4} --> {1,2,A,3,4})
- le polygone initial et final sont fermés (le premier sommet est aussi le dernier)
- le polygone est composé à minima de 3 sommets mais peut en contenir bien plus.
- les sommets sont exprimés dans une base 2D (type x y)
Aussi, je souhaite réaliser la manipulation sans avoir à tester si le nouveau sommet est inclu ou exclu de la surface du polygone initial (pas de "tests d'intersection")
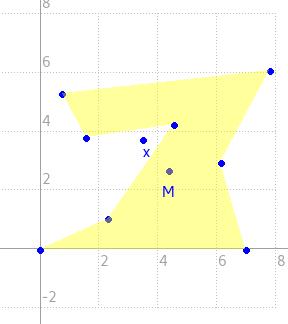
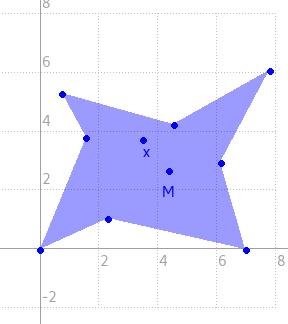
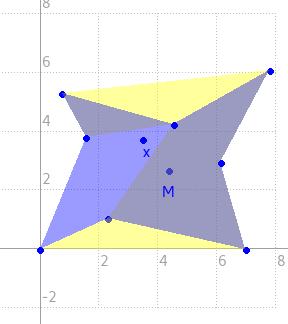
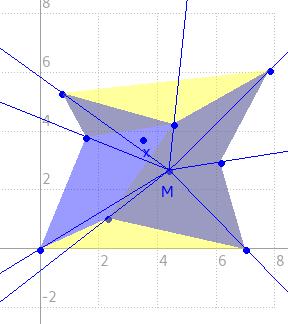
J'ai déjà tenté de réaliser cet exercice en testant le signe du produit vectoriel OI^OA (où O = barycentre du poly, I un sommet existant et A le nouveau sommet) pour chaque sommet 'I' du poly. Cependant, il est tout à fait possible que, selon la position du barycentre et la forme du polygone, on se retrouve avec plusieurs solutions dont certaines ne respectent pas les règles ci-dessus.
J'ai alors essayé de raisonner autour des angles IÔA pour chaque sommet 'I', mais je me retrouve confronté à la même problématique.
Pour info, le bout de code qui s'appuiera sur cet "algorithme" me servira justement à valider (ou non) une idée que j'ai afin de tester si un point est présent ou non au sein d'un polygone. Je sais qu'il existe d'autres méthodes que celle que je souhaite faire, mais là n'est pas la question.
Merci d'avance !












 Répondre avec citation
Répondre avec citation




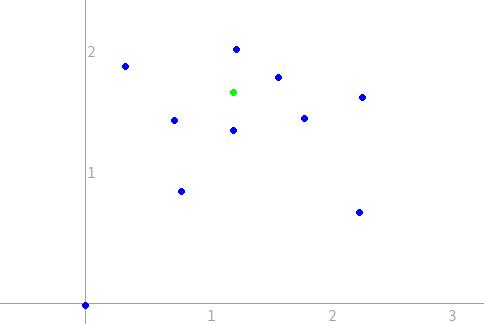
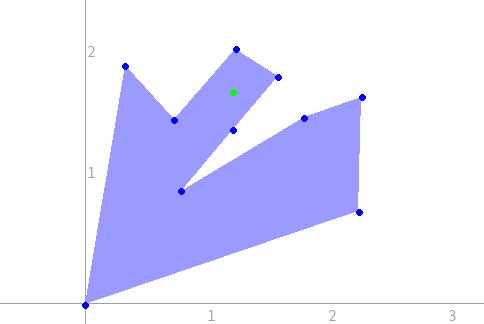
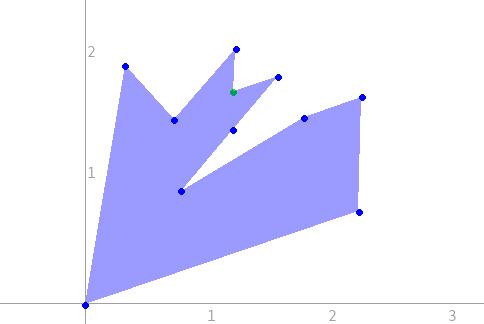
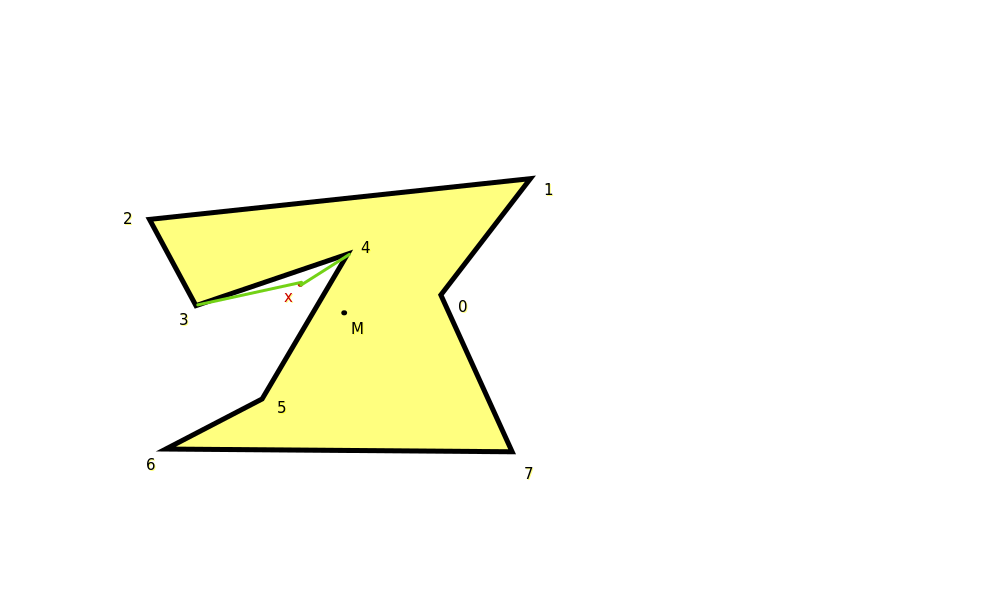

Partager