bonjour,
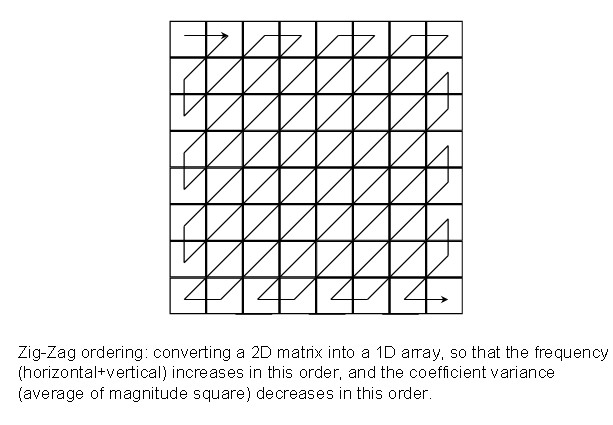
j'ai passée toute une journée a ecrire un algorithme pour une matrice en zig-zag mais aucun resultat
svp qu'elqu'un peut me proposer comment procède pour que je démarre
bonjour,
j'ai passée toute une journée a ecrire un algorithme pour une matrice en zig-zag mais aucun resultat
svp qu'elqu'un peut me proposer comment procède pour que je démarre

Partager