Discussion :

[Tokapi]

Bonjour à tous.

Actuellement sur un projet d'étude type mémoire, je suis bloqué sur le problème suivant qu'il me faut résoudre (et qui se résout, mais je ne trouve pas de documentation explicite sur le sujet) :

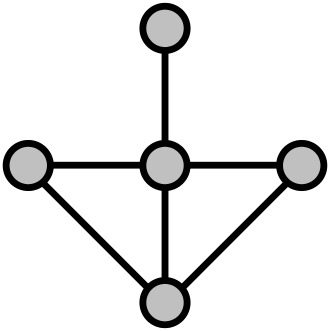
J'ai un graphe supposé planaire et codé par liste de voisins.
Je veux lui ajouter des arêtes jusqu'à ce qu'il devienne maximalement planaire, c'est-à-dire triangularisé (toutes ses faces sont des triangles) et planaire.

Si jamais vous pouviez m'aider sur ce sujet je vous en serais très reconnaissant.

Merci

[Flodelarab]

Bonjour

Je ne sais pas.

Intuitivement, je ferais ceci:

• Fais la liste des faces du graphe.
• Pour chaque face, distribue un sommet (n'importe lequel) sur les autres sommets de la face, si l'arête n'existe pas déjà.
• Pour les sommets non-impliqués dans une face:
  
  1. Trouver un voisin impliqué dans une face
  2. Relier le sommet non-impliqué à tous les sommets de la face dans laquelle est impliqué le voisin (n'importe laquelle)
  3. Recommencer à 1 jusqu'à ce que tous les sommets non-impliqués soit intégrés.
  4. Si aucun sommet n'a de voisin impliqué dans une face, choisir un sommet et le relier à tous les autres.
• Et ton graphe sera triangularisé.

[Tokapi]

Bonjour Flodelarab, merci pour ta réponse.

Effectivement c'est ce que j'avais pensé faire en premier lieu, mais je n'ai pas trop compris non plus comment trouver les faces d'un graphe (qui ne sont pas uniques), il faut a priori commencer par faire un tri cyclique des listes de voisins et je ne sais pas le faire : mon ex-prof de graphes m'a dit qu'un déterminant bien placé suffit mais je ne sais pas comment m'y prendre et je ne trouve pas de documentation explicite sur ce sujet-là non plus.

J'imagine que le tri cyclique dont il est question est juste un tri arbitraire des voisins mais je n'en suis pas bien sûr.

[tbc92]

J'essaie de comprendre la question...
J'imagine que le contexte, c'est une imprimante 3D. Tu as un volume (disons un cube pour avoir un exemple simple). Pour ce volume, tu connais les 12 arêtes (non ordonnées ...).
Et pour pouvoir imprimer ce cube, tu as besoin de définir sa surface comme une série de triangles.
Ton problème ressemble à ça ?

[Flodelarab]

les faces d'un graphe (qui ne sont pas uniques)

J'ai énormément de mal avec cette phrase. As-tu un exemple qui montre que les faces ne sont pas uniques ?

Le graphe suivant a 4 noeuds, 6 arêtes, 3 faces bien définies.


Non ?

[Tokapi]

@tbc92 : Non pas du tout. J'ai juste un graphe planaire que j'essaie de représenter planairement. Par exemple, ça sert à concevoir des circuits imprimés sur une carte sans croisements d'arrêtes.

@Flodelarab : Non, par exemple si tu dessines l'un des deux triangles dans l'autre triangle, c'est le même graphe mais les faces sont différentes.