Bonjour à tous.
Je vous propose un quizz portant sur les rapports entre fonctions et démonstrations. Il a été décidé de ne pas inclure ce quizz dans la série des défis fonctionnels à cause de son caractères plus théorique, et de ses objectifs assez différents.
Je tiens aussi à préciser que ce qui va être décrit ici n'est pas Anubis 2. Il y a bien sûr de nombreux points communs, mais ces concepts seront présentés dans Anubis 2 d'une manière beaucoup plus pratique pour l'utilisateur (avec pas mal de sucre syntaxique). Autrement-dit, vous devez considérer ce fil comme un jeu, et j'espère que vous vous amuserez bien. Les questions seront très progressives, et tout le monde peut essayer sans complexe.
Je remercie les modérateurs, et en particulier millie, pour le soutien qu'ils ont apporté à ce projet.
Aux nouvaux arrivants: Un résumé qui vous évitera de lire tout le fil se trouve ici. Par ailleurs, le deuxième post (ci-dessous) contient un glossaire des principales notions.
Je vais donc commencer par planter le décor. Nous sommes dans un langage fonctionnel 'imaginaire'. Dans ce langage, nous avons d'abord les types d'usage, c'est à dire les sommes, les produits et les types fonctionnels, ces types pouvant aussi être récursifs (avec certaines restrictions). Mais bien sûr, il y a d'autres types qui ne sont pas habituels dans un tel langage. Le premier d'entre eux est un type que je noterai O. Ce type a un seul constructeur, qui est défini par la règle suivante:
Je rappelle que le mot ``terme'' signifie tout simplement ``expression représentant une donnée''. C'est une construction du langage lui-même. C'est la dénomination usuelle en lambda-calcul. Une lambda-expression est un lambda-terme. Par contre, une expression représentant un type n'est pas un terme (du moins dans le langage qui nous occupe ici).Si T est un type, si x est une variable de type T, et si E est un terme de type O, pouvant contenir des occurrences libres de x, alors:
?x:T E
est un terme de type O. Dans ce terme, la variable x est liée.
Dans un langage typé, chaque terme a un type bien défini, qui est également le type de la donnée représentée par ce terme. Toutefois, il arrive qu'on emploie un autre vocabulaire que ``terme'' pour les termes de certains types. Ce sera le cas pour le type O, mais nous y reviendrons.
Pour ceux qui auraient un doute sur le sens de l'expression ``Dans ce terme, la variable x est liée.'', je précise qu'il s'agit du même concept que pour un lambda-terme. Dans le lambda-terme \x:T E, qu'on peut aussi écrire (x:T) |-> E, la variable x est liée. Voici donc la première question.
Question 1. Vous avez remarqué sans doute que pour construire un terme de type O, il nous faut un terme de type O. Dans ces conditions, on peut se demander s'il existe ne serait-ce qu'un seul terme de type O. La réponse est oui, et la question est d'en trouver un (et même plusieurs).











 Répondre avec citation
Répondre avec citation
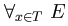



Partager