Salut à tous
svp aidez-moi à trouver l'application numérique de cet exercice auquel je vais appliquer mon traitement :
Soit un triangle équilatéral ABC dont le coté AC = a en cm.
on inscrit dans ce dernier un rectangle MNPQ
on pose BM=x
on propose de déterminer la valeur de x tel que l'aire du rectangle soit maximale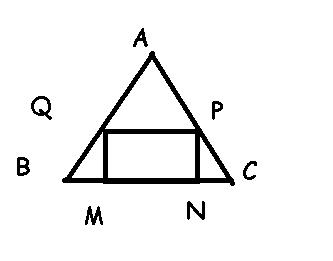














 Répondre avec citation
Répondre avec citation
Partager