1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
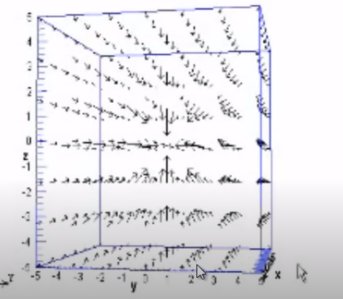
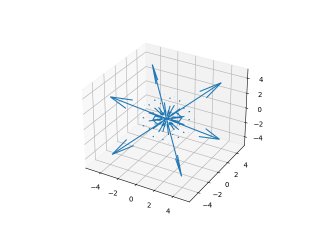
| # Simulation totalement fictive de la répartition de la chaleur dans une pièce en fonction de la position .
# Loi de diffusion T=10*exp-(x²+y²+z²)
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=[14,14])
ax = fig.gca(projection='3d')
# coordonnées des points de la simulation
x, y, z = np.meshgrid(np.linspace(-5, 5,10),
np.linspace(-5, 5, 10),
np.linspace(-5, 5, 10 ))
# Evolution de la température en fonction de la position dans la pièce
T = np.exp(-x ** 2) * np.exp(-y ** 2) * np.exp(-z ** 2)
# Calcul du gradient par le calcul de 3 dérivées partielles
u = -20* x * (np.exp(-x ** 2) * np.exp(-y ** 2) * np.exp(-z ** 2))
v = -20* y * (np.exp(-x ** 2) * np.exp(-y ** 2) * np.exp(-z ** 2))
w = -20* z * (np.exp(-x ** 2) * np.exp(-y ** 2) * np.exp(-z ** 2))
plt.grid()
# si on met True les vecteurs on la même longueur mais c'est plus joli
plt.quiver(x, y, z, u, v, w,normalize=True)
plt.show() |













 Répondre avec citation
Répondre avec citation



Partager