Résolution d'une EDP par la méthode des différences finies (Memory error)

**HanaChan** · 15/08/2019, 15h55

Bonjour,

J'ai besoin de résoudre par la méthode de différences finies l'équation dans le fichier ci-joint.
Schéma numérique.docx

Le but est d'avoir 3 vecteurs :

x composé de M+2 blocs identiques chacun comportant xi de i = 0 à i = N+2
y composé de M+2 blocs chacun comportant N+2 fois la valeur tj = j * Delta t
Z composé M+2 blocs chacun comportant les valeurs de u(xi,tj) pour tj fixé et i de 0 à N+2

Ces vecteurs seront utilisés pour le traçage du plot 3D de u(x,t).

Voici mon code :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import numpy as np
import scipy.sparse as sps
from scipy.sparse.linalg import spsolve
 
 
# Saisie des inputs par l'utilisateur
c = -1
e = 1
L = 1
T = 1
U0t = 2
ULt = 1
Ux0 = 1.5
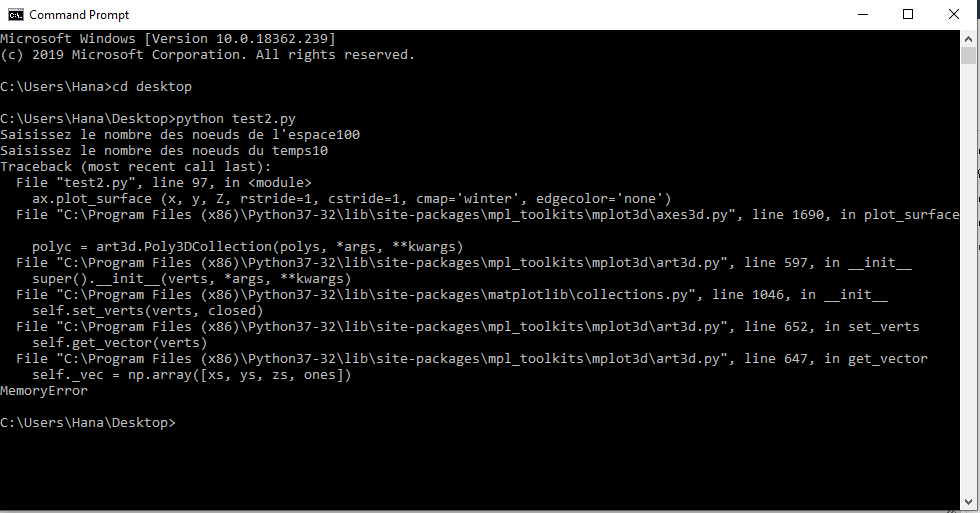
N = input ("Saisissez le nombre des noeuds de l'espace")
N = int (N)
M = input ("Saisissez le nombre des noeuds du temps")
M = int (M)
 
# Calcul du pas de l'espace
h = L/(N+1)
 
# Discrétisation de l'intervalle [0,L] selon le pas h
X = np.linspace (0.0,L,N+2)
 
 
# Calcul du pas du temps
t = T/(M+1)
 
 
# Remplissage de A matrice tridiagonale symétrique de taille N*N
def tridiag(P, Q, R, k1=-1, k2=0, k3=1):
    N = len(Q)
    return (sps.spdiags(P,-1,N,N) + sps.spdiags(Q,0,N,N) + sps.spdiags(R,1,N,N))
 
P = (1/h**2)*np.ones(N)
 
Q = (c - 2/h**2)*np.ones(N)
 
A = sps.csc_matrix(tridiag(P,Q,P))
 
 
# Remplissage de B vecteur colonne de taille N
B = np.zeros(N)
B[0] = (1/h**2)*U0t
B[N-1] = (1/h**2)*ULt
 
 
# Initialisation de Uj à l'instant tj=0
U = Ux0*np.ones(N)
 
# Nouvelle A
A = sps.csc_matrix((e/t)*np.eye(N) - A)
 
 
# Intialisation de x, y = t et Z = u (x,t) à l'instant y = t = 0
 
x = X
y = np.zeros(N+2)	
z = np.insert (U,0,[U0t])
z = np.append (z,[ULt])
Z = z
 
# Calcul de Uj+1 à partir de Uj
 
for j in range (1,M+2):
	# Insertion du jème bloc des xi  
	x = np.append(x,X)
	# Insertion du jème bloc de tj 
	y = np.append(y,[j*t*np.ones(N+2)])
	# Calcul de Uj à partir de Uj-1
	V = (e/t)*U + B
	U = spsolve(A,V)
	U = np.ravel(U)
	# Insertion de u(0,tj) et u(L,tj)
	z = np.append (U,[ULt])
	z = np.insert (z,0,[U0t])
	# Insertion du jème bloc de u(xi,tj)
	Z = np.append (Z,z)
 
 
# Traçage du plot 3D de u(x,t)
 
Z = np.reshape(Z,((N+2)*(M+2),1))
 
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
 
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.plot_wireframe(x, y, Z, color='green')
ax.set_xlabel('x')
ax.set_ylabel('t')
ax.set_zlabel('u')
ax.plot_surface (x, y, Z, rstride=1, cstride=1, cmap='winter', edgecolor='none')
 
plt.show()

Pour N = 10 et M =10, le code marche parfaitement. Mais, pour N = 100 et M =10, j'obtiens un Memory error.
Nom : 1.PNG
Affichages : 1027
Taille : 36,2 Ko

Comment faire pour résoudre ce problème ?

Merci de votre aide

**lg_53** · 16/08/2019, 12h34

Le problème est trop gros pour votre ordinateur, c'est pour ca que vous avez le MemoryError.
Essayez de monter progressivement les paramètres pour confirmer cela.

En meme temps quand on utilise numpy (ce qui est bien pour le calcul scienifique), mais qu'on fait des append et des inserts dans tous les sens, ca ne m'étonne pas de rencontrer ce genre de problème, pour des dimensions qui ont l'air somme toutes raisonnables. Il faut banir ces 2 mots append et insert.
Vous avez un array, vous savez la taille qu'il doit faire à la fin. Et bien vous lui donnez directement la bonne taille, et vous le remplissez de 0. Et au fur et à mesure, après, vous remplissez les données

Typiquement, pour obtenir un array des carrés par exemple (np.array([0,1,4,9,...])), on n'écrit surtout pas ca :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
x= np.array([])
for k in range(10):
   x = np.append(x,k*k)

mais ca

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
x= np.zeros((10,))
for k in range(10):
   x[k] = k*k

**HanaChan** · 16/08/2019, 16h58

Bonjour,

merci de votre réponse

En fait, lorsque je supprime les lignes du traçage du plot 3D, et que je fixe M à 100, le code marche jusqu'à N = 7943.

En éliminant tous les insert et append (voir code ci-dessous), le code marche jusqu'à N = 7957 (toujours pour M = 100 fixé).

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Initialisation de Uj à l'instant tj=0
U = Ux0*np.ones(N)
 
# Nouvelle A
A = sps.csc_matrix((e/t)*np.eye(N) - A)
 
# Insertion du 1er bloc de Z = u (xi,0) pour tj = 0 
Z = np.zeros((N+2)*(M+2),)
Z[0] = U0t
for i in range (1,N+1):
	Z[i] = Ux0
Z[N+1] = ULt
 
# Calcul de Uj à partir de Uj-1
 
for j in range (1,M+2):
	# Calcul de Uj à partir de Uj-1
	V = (e/t)*U + B
	U = spsolve(A,V)
	# Insertion du (j+1)ème bloc de Z = u(xi,tj) avec tj fixé 
	Z[j*(N+2)] = U0t
	for i in range (1,N+1):
		Z[i+j*(N+2)] = U [i-1]
	Z[N+1+j*(N+2)] = ULt
 
# Remplissage des vecteurs X et Y de taille (N+2)*(M+2) 
X = np.zeros((N+2)*(M+2),)
Y = np.zeros((N+2)*(M+2),)
for j in range (M+2):
	for i in range (N+2):
		X[i+j*(N+2)]=i*h
		Y[i+j*(N+2)]=j*t

Par contre, lorsque j'ajoute le traçage du plot au code :

pour M fixé à 10, le plot n'est plus affiché pour N > 489 (j'obtiens un MemoryError)
pour M fixé à 100, le plot n'est plus affiché pour N > 55

**wiztricks** · 16/08/2019, 19h56

Salut,

Avec un adressage 64bit (enfin pas si tant mais quand même) on est toujours surpris d'arriver à dépasser la capacité mémoire... surtout "virtuelle" (qui elle est pour le coup presque un espace adressable avec 64 bits).

Mais c'est le système d'exploitation qui gère çà et qui dit à Python: je ne peux pas te donner la mémoire que tu veux et çà plante avec Memory Error.

Pour çà il se base en général sur la mémoire (RAM) disponible et sur la place disponible côté fichiers de pagination (s'il est nécessaire d'associer à la page de mémoire physique qu'on va octroyer un "backing store" i.e. de la place dans le fichier de pagination s'il faut en sauvegarder le contenu pour ré allouer - plus tard - la page à un autre processus).

Bien sûr la solution est d'ajouter de la mémoire physique (de la RAM). Après l'opération, le système retaille en général les fichiers de pagination à k * taille de la RAM.
La solution du pauvre est de se contenter d'augmenter la taille des fichiers de pagination (ou d'en ajouter). S'il n'y a pas assez de mémoire physique, le programme va ramer (à cause des entrées sorties disque) mais devrait fonctionner.

edit: après regardé plus en détails l'image que vous avez posté initialement, vous semblez utiliser une mouture 32 bits de Python sur un engin qui dispose de 64 bits d'espace d'adressage. Il faut déjà commencer par migrer tout çà en 64 bits.

- W

**lg_53** · 19/08/2019, 09h51

Envoyé par HanaChan

En fait, lorsque je supprime les lignes du traçage du plot 3D, et que je fixe M à 100, le code marche jusqu'à N = 7943.

En éliminant tous les insert et append (voir code ci-dessous), le code marche jusqu'à N = 7957 (toujours pour M = 100 fixé).

Du coup ce nb'est pas une très belle illustration du propos que je tenais sur les insert et append. Sachez que là ca se passe donc plutot bien pour vous. Dans d'autres cas ca peut aller du simple au double voire triple ou quadruple !

Vous avez donc avancé en identifiant que c'est le plot qui consomme beaucoup de mémoire.
Pourquoi faire une surface ET un wireframe ? Vous avez essayez de vous contentez de seulement l'un des 2, et d'analyser à nouveau la limite mémoire ?
Et sinon, pourquoi ne pas opter pour un plot moins gourmand, de type 2D couleur ? C'est suffisant pour avoir toute l'information.
On peut utiliser notamment pcolor, ou pcolormesh

https://courspython.com/visualisation-couleur.html

**HanaChan** · 19/08/2019, 17h45

Merci de vos réponses.

En fait, vous avez raison, j'avais installé la version 32 bits de Python alors que je travaille avec un pc sous Windows 64 bits. Avec la version 64 bits, les valeurs de Z sont calculées même pour N = 10000 et M =100.

Côté plot 3D, j'avais fait des essais en gardant juste le plot Wireframe, je n'ai pas noté jusqu'à quelle valeur de N ça marche pour M fixé à 10 puis à 100, mais ce dont je me rappelle c'est que à un certain moment, le graphe devient difficile à comprendre ...

J'ai essayé la visualisation 2D en couleur, c'est beaucoup plus rapide

Résolution d'une EDP par la méthode des différences finies (Memory error)

Calcul scientifique Python

Vue hybride

Discussions similaires

Partager

Partager