Discussion :

[plglef]

Bonjour
j'ai un petit souci: le but étant d'avoir deux cribles équivalents; pour cribler de N à 2N "Goldbach" et de 7 à N "Eratosthène" :
Afin de justifier les deux fonctions relatives à : et
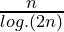
Voici la partie que je voudrai modifier pour utiliser GCrible de Goldbach dans Ecrible Eratosthène :

Voici la partie du progr origine que je dois modifier:
1) On remplacera la première ligne de def eratostene

Code python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
def eratostene(n):
    n = int((2*n)**0.5) par n = int(n**0,5)

*****************************

Code python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
 
def GCrible(premiers, n, fam):
    start_crible = time()
 
    # On génère un tableau de N/30 cases rempli de 1
    crible = n//30*[1]
    lencrible = len(crible)
 
    # On calcule les restes: ri = 2*n/pi
    nbpremiers = len(premiers)
    n2 = 2*n
 
    for i, premier in enumerate(premiers):
        reste = n2 % premier
	# tant que ri % 30 != fam on fait ri += 2pi
        if reste % 2 == 0:
            reste += premier
        pi2 = 2*premier
        while reste % 30 != fam:
            reste += pi2
        # Ensuite on divise ri par 30 pour obtenir l'indexe
        reste //= 30
        # On crible directement avec l'index
        for index in range(reste, lencrible, premier):
            crible[index] = 0

#################################################################

Voici la partie que je veux modifier mais qui ne marche pas :

là on crible pareil, mais on n’a plus besoin de calculer le reste r de 2n par premiers…
Il faut par contre, une fonction tableMulti pour calculer le produit de pi = 1,7,11,13,17,19,23,29
Par premiers, et que l’on réitèrera. Pour chaque premier…
De sorte que j = pi * premiers , pour chaque premier , on calculera ensuite l’index…pour cribler ; au lieu du reste, dans Goldbach.
et ensuite que : j %30 == 1

exemple :
n = 3000 on a initialiser les 1 , 3000 /30 = 100, soit 100 cellules de 1
je prends premiers = 7

je calcule J = pi *7……….donc 8 produits au maximum, en vérifiant si j %30 == 1 car on crible la fam 1.

7*1 , 7*7, 7*11, 7*13 == 1%30 ; donc ok et je n’ai pas besoin d’aller jusqu’à pi = 29 pour calculer 7*29, d’accord….
Puis je vais calculer son index j = 91 , 91//30 = 3

Je positionne cellule 3 et je crible par pas de premiers = 7…de 3 à n//30 on remplace les [1] par [0] tous les 7 pas….etc… on réitère avec premiers = 11…..premiers <= sqrt de n et non de 2n, car c’est Eratosthène….modulo 30

**************************

Code python :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
 
def ECrible(premiers, n, fam):
    start_crible = time()
 
    # On génère un tableau de N/30 cases rempli de 1
    crible = n//30*[1]
    lencrible = len(crible)
 
    # On calcule le produit : j = pi * premiers, pour partir de l’index de ce produit
    nbpremiers = len(premiers)
    pi = 1,7,11,13,17,19,23,29
 
    for i, premier in enumerate(premiers):
        def tableMulti (premiers,pi):
            j = pi * premiers
	# tant que j % 30 != fam on fait pi * premiers
        while j % 30 != fam:
            tableMulti(pi*premiers)
        # Ensuite on divise j par 30 pour obtenir l'indexe
        if j % 30 == fam:
            j //= 30
        # On crible directement à partir de l'index
        for index in range(j, lencrible, premiers):
            crible[index] = 0

le reste du programme, ne change donc pas.

message d’erreur
Traceback (most recent call last):
File "E:\Documents\Conjecture de Goldbach\Crible_G.T.Y_modulo30.py", line 85, in <module>
main()
File "E:\Documents\Conjecture de Goldbach\Crible_G.T.Y_modulo30.py", line 80, in main
ECrible(premiers, n, 1)
File "E:\Documents\Conjecture de Goldbach\Crible_G.T.Y_modulo30.py", line 55, in ECrible
while j % 30 != fam:
UnboundLocalError: local variable 'j' referenced before assignment
>>>


Et ensuite je le ferai ...si possible...en C++ afin de le publier à la suite de ce fil .....

[VinsS]

Salut,

Le message d'erreur est assez clair il me semble.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
 
    for i, premier in enumerate(premiers):
        def tableMulti (premiers,pi):
            j = pi * premiers
 
        while j % 30 != fam:
            tableMulti(pi*premiers)

j est définit dans une fonction et est inconnu au départ de ta boucle.

Ceci dit, pi est un tuple, donc que veux-tu faire avec j = pi * premiers ?