Discussion :

[doinier]

bonjour à tous !!!
tous d'abord je m'excuse pour se long silence.
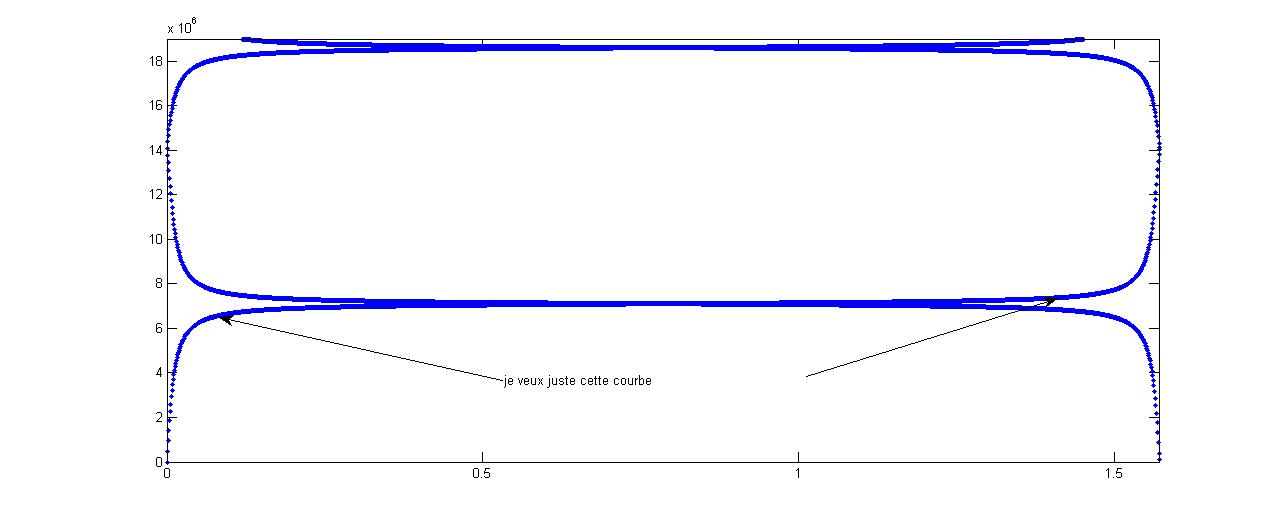
en fait, je suis confronté à un problème qui me torture depuis plus de 4 mois.
le problème c'est: je n'arrive pas à tracer la dérivé de la courbe comme le montre le code matlab ci-joint.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
gp=0
B1=5e-6;
B2=7e-6;
C0n=110e-12;
%Cs=95e-12;
Cso=0;
B=B1.*B2./(B1+B2);
 
j=1;
for kp=0:0.001:pi/2
 
    Q1=-(-2.*Cso^2+(2.*Cso+C0n)^2)^2;
    Q2=-8.*cos(2.*kp).^2.*Cso^3./B-(2.*(-2.*C0n./B-2.*Cso./B-gp^2));
    Q3=4.*cos(2.*kp).^2.*(2.*Cso^2./(B1.*B2)+Cso^2./B^2)-(2.*(1./B^2-1./B1^2-1./B2^2)).*(-2.*Cso^2+(2.*Cso+C0n)^2);
    Q4=-8.*cos(2.*kp).^2.*Cso./(B1.*B2.*B);
    Q5=-(1./B^2-1./B1^2-1./B2^2)^2+4.*cos(2.*kp).^2./(B1^2.*B2^2);
 
    pol=[Q1 Q2 Q3 Q4 Q5];
 
    eigen=roots(pol)
 
    for n=1:length(eigen)
        if real(eigen(4))>=0
            OME(j,1)=kp   ;
            OME1(j,2) =real(sqrt(eigen(4)));
            j=j+1
        end
    end
end
%\\\\\\\\\\\\\\\\\\\\\courbe proprement dite\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
 
plot(OME(:,1),OME1(:,2),'.')
 
%/////////////////////tracé de la dérivé//////////////////////////////////
 
uk=diff(OME1(:,2))./diff(OME(:,1))% définition de la dérivé
 
plot(OME1(length(OME1)-1),uk)

à chaque fois ça me donne une droite verticale. je voudrais que vous y jetiez un cout d'oeil please

[Invité]

Bonsoir,

La partie OME1(length(OME1)-1) dans la ligne

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

plot(OME1(length(OME1)-1),uk)

ne représente qu'une seule valeur, tu traces donc toutes les valeurs dans uk sur la même abscisse.

Ne voulais-tu pas quelque chose comme :

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
plot(OME1(1:end-1,1), uk) % première colonne
plot(OME1(1:end-1,2), uk) % deuxième colonne

?
[EDIT]Plutôt OME que OME1 en abscisses d'après ce que je vois.

[doinier]

Merciiiiii, Winjerome là je commence à avoir une lieur d'espoir c'était parfait

[doinier]

bonsoir !!!
tous d'abord je m'excuse pour le silence. je voudrais ne tracer qu'une seule courbe celle indiquée sur le fichier joint. mais à chaque fois que je

prend n=1,2,3,4,5,6...etc, j'ai comme un mélange de courbe pourtant je n'en veux qu'une seule, celle indiquée sur la courbe

voilà mon code.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
C0=540e-12;
 
%*************************************************************
L2=14e-6;
L1=28e-6;
S1=5;
S2=S1*L2/L1;
 
I1=1/(L1*C0);
I2=1/(L2*C0);
 
Ir1=S1/L1;
Ir2=S2/L2;
 
It=I1+I2;
IT=I1+I2;
 
 
j=1;
for k=0:0.001:1.6
%----------------déclaration du polynôme-----------------------------------
Q8=I2.^2.*I1.^2.*(1-cos(2.*k).^2);
Q6=(-2.*Ir1.*Ir2-4.*It).*I2.^2.*I1.^2.*(1-cos(2.*k).^2)-(Ir1+Ir2).^2.*I2.^2.*I1.^2.*cos(2.*k).^2;
Q4=(-2.*I1.^2-2.*I2.^2+2.*It.^2+(-Ir1.*Ir2-2.*It).^2).*I2.^2.*I1.^2.*(1-cos(2.*k).^2)-(2.*(-Ir1.*It-Ir2.*It)).*(Ir1+Ir2).*I2.^2.*I1.^2.*cos(2.*k).^2;
Q2=(2.*(-I1.^2-I2.^2+It.^2)).*(-Ir1.*Ir2-2.*It).*I2.^2.*I1.^2.*(1-cos(2.*k).^2)-(-Ir1.*It-Ir2.*It).^2.*I2.^2.*I1.^2.*cos(2.*k).^2;
Q0=+(-I1.^2-I2.^2+It.^2).^2.*I2.^2.*I1.^2.*(1-(cos(2.*k)).^2);
 
 
pol=[ Q8 0 Q6 0 Q4 0 Q2 0 Q0];
%--------------------------------------------------------------------------
%------------------Résolution du polynôme----------------------------------
eigen=roots(pol);
 
for n=1:numel(eigen)  
 
if  real(eigen(n))>=0 
 
  OMER(j,1)=k ;      % range les éléments dans une matrice 
 
  OME1(j,1)=real(eigen(n)); % range la partie réelle de eigen dans une matrice
 
  j=j+1;
 
end
 
end
end
%---------tracé des courbe----------------
plot(OMER(:,1),OME1(:,1),'.')

et aussi je devrais avoir 8 solutions, mais je n'en n'ai que 6, car pour n=7,8; y a rien. pourtant

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

length(eigen)

me donne 8

s'il vous plaît help me.

[lucaswalker]

Bonjour,

Le problème est que pour k = 0 et k = pi/2 la courbe est verticalement asymptotique.

Essayez avec des valeurs de k excluant ces points (for k=0.005:0.001:1.565) par exemple, et on retrouve la jolie courbe. Au passage il y a bien une unique courbe, mais avec les asymptotes tous les points sont concentrés et on comprend plus rien.

[doinier]

bonjour lucaswalker!!!

merci pour ton intervention, j’essaie pour voir. mais je me réserve de boucler cette discussion car quelqu'un pourrait entre temps avoir quelque chose à ajouter. merci encore.

[doinier]

bonjour lucaswalker,

j'ai essayé le code suivant pour choisir la courbe sélectionner mais ça n'affiche que le deuxième bloc:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
 plot(OMER2(:,1),OME1(:,1),'.')
%    hold on
%    ylim([0 7130000])
%    xlim([0 0.8])
%%%%% deuxième bloc%%%%%%
%      hold on
%    plot(OMER2(:,1),OME1(:,1),'.')
%     ylim([7130000 14110000])
%     xlim([0.8 1.57])
%   hold off

merci d'y jeter un coup d’œil s'il te plait

[lucaswalker]

le plot ne trace qu'une unique courbe, pour obtenir le plot que tu veux il faut par conséquent sélectionner les bonnes valeurs dans tes vecteurs. Le code suivant peut faire l'affaire:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
%---------tracé des courbe----------------
hold on
plot(OMER(2:2:length(OME1(:,1))/2,1),OME1(2:2:length(OME1(:,1))/2,1),'.')
plot(OMER(length(OME1(:,1))/2+1:2:length(OME1(:,1)),1),OME1(length(OME1(:,1))/2+1:2:length(OME1(:,1)),1),'.')
ylim([0 14000000])
xlim([0 1.6])

[doinier]

Merci lucaswalker, ça fonctionne .

mais je voudrais stp que tu m'explique ses lignes . là je pourrais modifier les zone à ma guise c-à-dire

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
plot(OMER2(2:2:length(OME1(:,1))/2,1),OME1(2:2:length(OME1(:,1))/2,1),'.')
plot(OMER2(length(OME1(:,1))/2+1:2:length(OME1(:,1)),1),OME1(length(OME1(:,1))/2+1:2:length(OME1(:,1)),1),'.')