Voici une implémentation Java de l'algorithme "Snake" (contour actif).
L'algorithme Snake permet de tracer le contour d'une zone irrégulière en déformant progressivement une courbe de départ. Pour plus d'informations, je vous conseille l'article de khayyam90.
La classe Snake (attributs+constructeur)
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
Les méthodes de l'algorithme "snake"
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
Les méthodes des fonctions d'energie:
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
Les méthodes du mécanisme d'auto-adaptation:
Code java : Sélectionner tout - Visualiser dans une fenêtre à part
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
Utilisation:
Le constructeur de la classe Snake a besoin des paramètres suivants:
- int width,height: la taille de l'image (et des deux tableaux suivants)
- int[][] gradient: un tableau contenant la norme du gradient pour chaque pixel [x][y]
- int[][] flow: un tableau contenant la norme du vecteur de flux pour chaque pixel [x][y].
En pratique, on peut utiliser la carte des distances jusqu'au pic de gradient le plus proche- Point... points: la liste des points constituant le snake initial
La méthode publique "loop()" fait évoluer le snake jusqu'a convergence et retourne la liste des points du snake final.












 Répondre avec citation
Répondre avec citation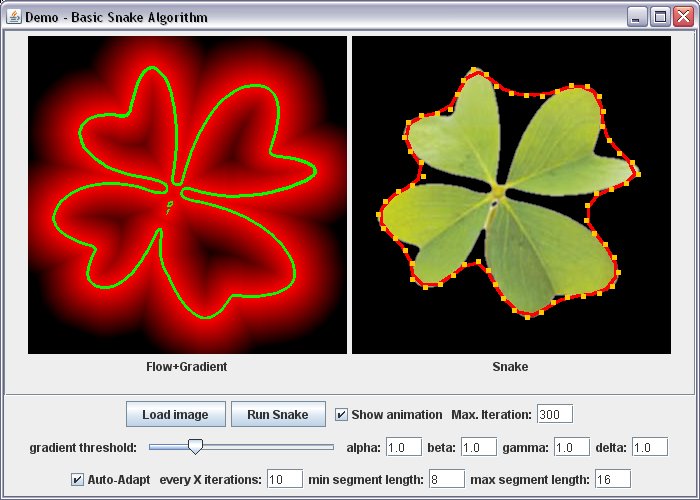














Partager