conjectureCollatz.py
"""#python
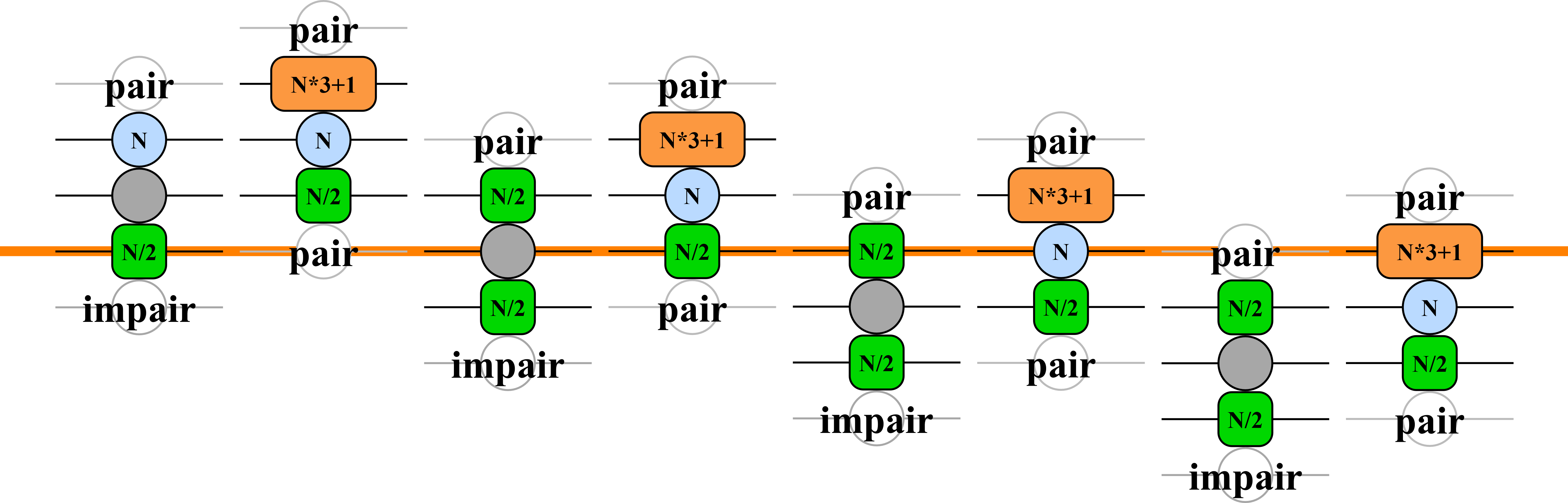
Bonjour, c'est Bing. Je peux vous aider à trouver des informations sur les nombres pairs et impairs. 😊
Vous avez décrit une règle qui s'applique aux nombres entiers. Pour un nombre pair, on le divise par deux.
Pour un nombre impair, on le multiplie par trois et on ajoute un. Par exemple :
- Si le nombre est 4, il est pair, donc on le divise par deux : 4 / 2 = 2
- Si le nombre est 5, il est impair, donc on le multiplie par trois et on ajoute un : 5 x 3 + 1 = 16
Cette règle est connue sous le nom de **conjecture de Collatz** ou de **problème de Syracuse**.
C'est un problème mathématique qui n'a pas encore été résolu.
Il consiste à se demander si, en appliquant cette règle à n'importe quel nombre entier positif,
on finit toujours par obtenir 1.
Par exemple, si on part de 6, on obtient la suite suivante :
- 6 est pair, donc on le divise par deux : 6 / 2 = 3
- 3 est impair, donc on le multiplie par trois et on ajoute un : 3 x 3 + 1 = 10
- 10 est pair, donc on le divise par deux : 10 / 2 = 5
- 5 est impair, donc on le multiplie par trois et on ajoute un : 5 x 3 + 1 = 16
- 16 est pair, donc on le divise par deux : 16 / 2 = 8
- 8 est pair, donc on le divise par deux : 8 / 2 = 4
- 4 est pair, donc on le divise par deux : 4 / 2 = 2
- 2 est pair, donc on le divise par deux : 2 / 2 = **1**
On a obtenu **1** au bout de **8** étapes. On dit que le temps de vol de **6** est de **8**.
La conjecture de Collatz affirme que pour tout nombre entier positif,
il existe un temps de vol fini qui permet d'obtenir **1**.
Mais personne n'a réussi à le démontrer ni à le réfuter.
Trouvez-vous ce problème intéressant ?
"""
# Recherche type de nombre (*3)
for i in range(1, 60, 2):
ii = i * 3 + 1
print('i:', i, 'ii:', ii)
'''i: 1 ii: 4
i: 3 ii: 10
i: 5 ii: 16
i: 7 ii: 22
i: 9 ii: 28
i: 11 ii: 34
i: 13 ii: 40
i: 15 ii: 46
i: 17 ii: 52
i: 19 ii: 58
i: 21 ii: 64
i: 23 ii: 70
i: 25 ii: 76
i: 27 ii: 82
i: 29 ii: 88
i: 31 ii: 94
i: 33 ii: 100
i: 35 ii: 106
i: 37 ii: 112
i: 39 ii: 118
i: 41 ii: 124
i: 43 ii: 130
i: 45 ii: 136
i: 47 ii: 142
i: 49 ii: 148
i: 51 ii: 154
i: 53 ii: 160
i: 55 ii: 166
i: 57 ii: 172
i: 59 ii: 178'''
#
'''
En faisant nombre_impair par trois plus un, on obtient toujours un produit pair.
Chaque nombre pair est divisé par deux, et les nombres pairs sont les plus nombreux à être sollicités.
Il est normal que la division d'une quantité plus importante de nombre pairs par deux résulte un.'''
nombre = int(input('Entrez un nombre entier :'))
print('Nombre initial =', nombre)
quantite_pairs = quantite_impairs = 0
while nombre != 1:
if nombre%2 == 0:
nombre /= 2
quantite_pairs += 1
else:
nombre = nombre * 3 + 1
quantite_impairs += 1
nombre_termes = quantite_pairs + quantite_impairs
print('nombre =', nombre, 'quantite_pairs =', quantite_pairs, 'quantite_impairs =', quantite_impairs,
'nombre_termes =', nombre_termes)
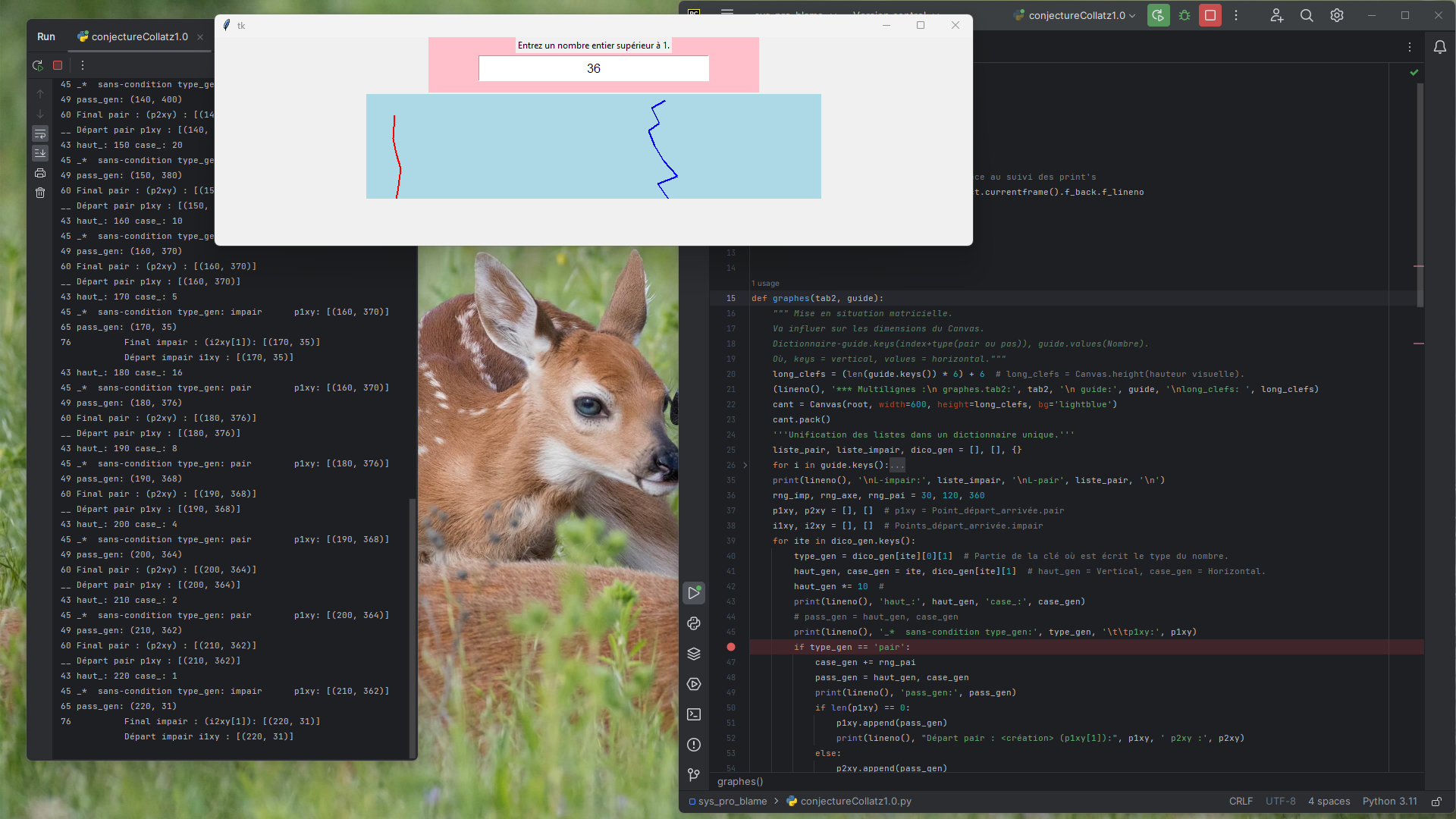
'''Entrez un nombre entier :1598753
Nombre initial = 1598753
nombre = 1.0 quantite_pairs = 51 quantite_impairs = 19 nombre_termes = 70'''











 Répondre avec citation
Répondre avec citation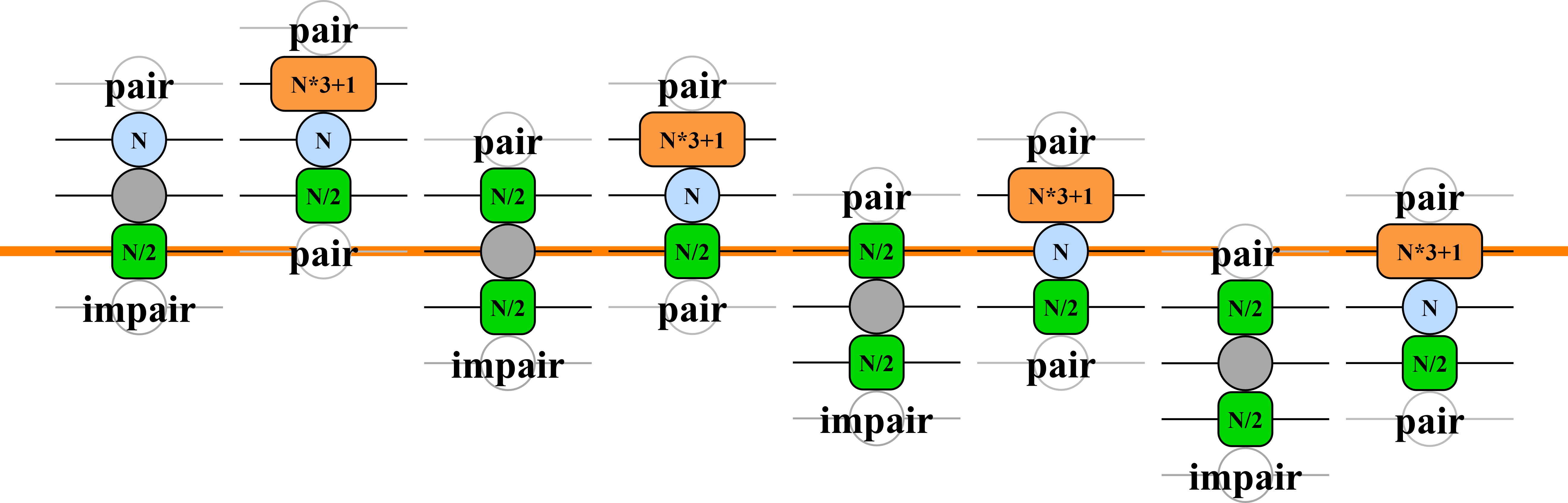











![Nom : Toumic [2023-05-14] B.png
Affichages : 231
Taille : 18,1 Ko](https://www.developpez.net/forums/attachments/p638654d1684050896/club-professionnels-informatique/taverne-club-humour-divers/humour-informatique/tiens-collez-point-py/toumic-2023-05-14-b.png/)











Partager