Discussion :

[tabkelm]

bonjour,

Sur Scilab,j'ai 4 listes (de longueur N) de points
L1=[x1,x2,x3,x4,x5,x6,....,xN]
L2=[y1,y2,y3,y4,y5,y6,...,yN]
L3=[f'(x1),f'(x2),f'(x3),.....,f'(xN)]
L4=[f''(x1),f''(x2),f''(x3),.....,f'(xN)]
Quelles sont les lignes de commande à entrer pour obtenir le polynôme P de degré 3n ?
tels que:
pour tout i de [1,N],
P(xi)=yi
P'(xi)=f'(xi)
P''(xi)=f''(xi)

merci de votre aide

[mottelet]

bonjour,

Sur Scilab,j'ai 4 listes (de longueur N) de points
L1=[x1,x2,x3,x4,x5,x6,....,xN]
L2=[y1,y2,y3,y4,y5,y6,...,yN]
L3=[f'(x1),f'(x2),f'(x3),.....,f'(xN)]
L4=[f''(x1),f''(x2),f''(x3),.....,f'(xN)]
Quelles sont les lignes de commande à entrer pour obtenir le polynôme P de degré 3n ?
tels que:
pour tout i de [1,N],
P(xi)=yi
P'(xi)=f'(xi)
P''(xi)=f''(xi)

merci de votre aide

Bonjour,

En général l'interpolation d'Hermite ne considère que les deux premières conditions P(xi)=yi=f(xi) et P'(xi)=f'(xi). On peut s'en tirer en généralisant le calcul par différences divisées à la recherche du polynôme d'interpolation d'Hermite "généralisé" comme indiqué pages 8-9 du document suivant : http://irma.math.unistra.fr/~mehrenb...umL3S6Phys.pdf

Voici le code Scilab que l'on pourrait écrire en modifiant un code existant calculant les différences divisées, ici en répétant trois fois les les valeurs des xi et des yi, et en insérant au bon moment les valeurs connues des dérivées premières et secondes. On obtient les coefficients du polynôme dans la base de Newton, c'est pour cela qu'il faut les recalculer dans la base canonique (les monômes). L'exemple choisi est l'interpolation du sinus sur [0,2*pi] avec seulement trois points.

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
function [T,c]=calDifDiv(t,y,d,s)  
    n = length(t)-1;
    N = 3*(n+1);
    c = zeros(N,1);
    T = zeros(N,1);
    c(1:3:$) = y; c(2:3:$) = y; c(3:3:$) = y;
    T(1:3:$) = t; T(2:3:$) = t; T(3:3:$) = t;
 
    for i = 2:N
        j = i:N;
        c(j) = (c(j-1)-c(j))./(T(j-i+1)-T(j));
        if i == 2
            c(2:3:$) = d; c(3:3:$) = d;        
        elseif i == 3
            c(3:3:$) = s/2;
        end
    end
end
 
t = [0;%pi;2*%pi];
y = sin(t);
d = cos(t);
s = -sin(t);
 
[T,c]=calDifDiv(t,y,d,s)
 
// conversion base de Newton -> base canonique
t = poly(0,"t");
p = c(1);
m = 1;
for i=2:3*length(y)
    m = m * (t-T(i-1));
    p = p + c(i)*m;
end
 
disp(p)
 
clf
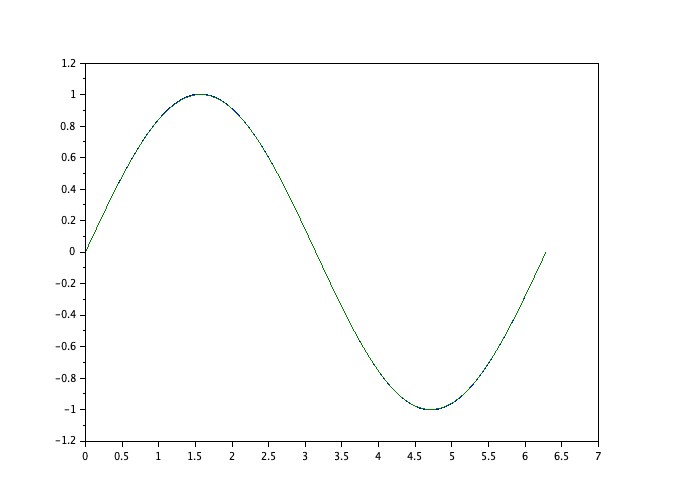
u = linspace(0,2*%pi,100)';
plot(u,horner(p,u),u,sin(u))

S.