Bonjour, 
Je me demande si le problème n'a pas été mal formulé dès le départ, faute d'une représentation géométrique.

Envoyé par
Pecose

... Mon projet et de trouver la distance d'un objet en comparent 2 photos.
Un réseau de neurones s'occupe dans un premier temps, d'identifier l'objet et me renvoie deux points (haut/gauche et bas/droite) pour situer cette objet sur cette photo.
D'un autre côté, je créé une position à mon téléphone grâce au gyroscope et à l’accéléromètre.
Ensuite, je créé un horizon arbitraire sur lequel je met ma photo et je me retrouve, lorsque j'ai deux photo, avec deux yeux et deux objets, donc, deux segments qui sont:
- œil_1 à objet_1
- œil_2 à objet_2 ...
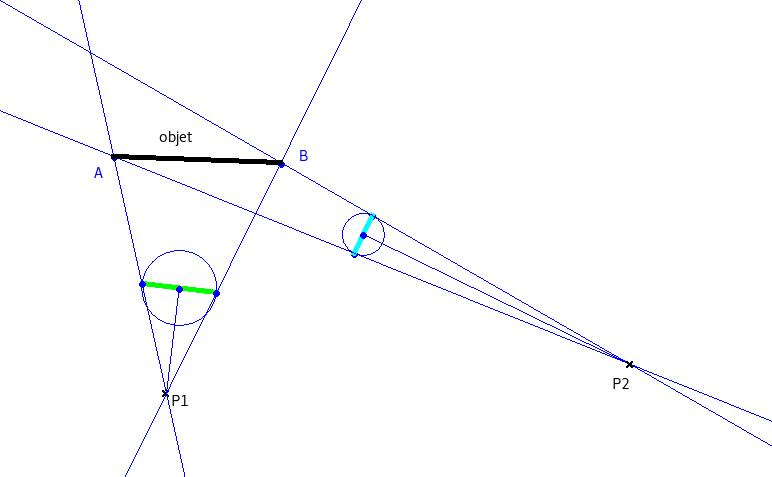
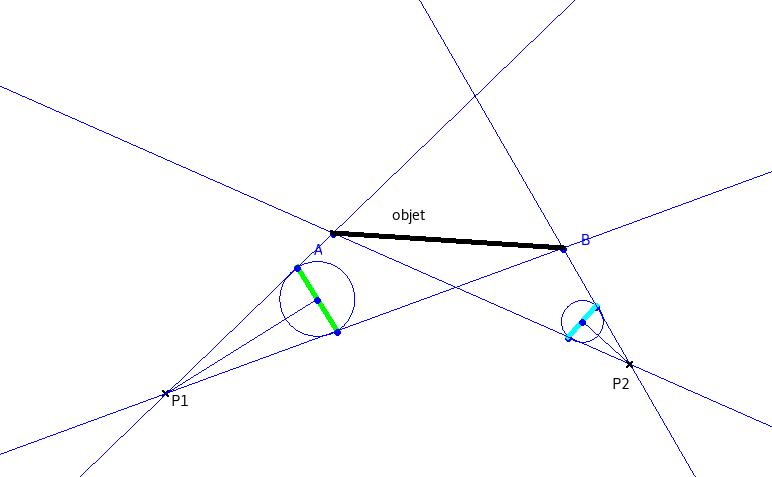
Il s'agit initialement (si j'ai bien compris) de la restitution spatiale d'un objet réduit à deux points, à partir de deux photographies prises selon des directions différentes. Or un glissement de sens intervient dès la fin de l'énoncé, qui gauchit la discussion vers la recherche de la distance entre deux objets.
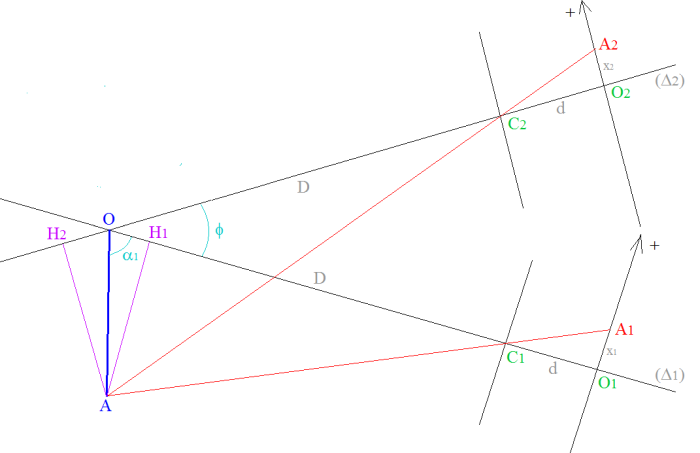
Supposons l'axe optique (Δ1 ou Δ2) de l'objectif maintenu horizontal, et son centre optique à distance fixe (D = OC1 = OC2) d'un point (O) proche de l'objet (AB) - on pourra par la suite y revenir.
Les images (A1, A2) du point objet (A) résultent de la projection centrale de ce point sur deux plans normaux à l'axe optique correspondant, et placés à une distance d = C1O1 = C2O2 du centre optique de l'objectif, distance très proche de la distance focale.
Voici ce que donne la projection orthogonale de l'ensemble sur un plan horizontal - cette transformation ne modifiant pas les relations données par la suite:
Il y a bien deux paires de triangles de même forme, dont la similitude s'exprime par les relations:
(H1A)/(O1A1) = (C1H1)/(C1O1) ;
(H2A)/(O2A2) = (C2H2)/(C2O2) ,
et (en convenant de poser L = OA) complétées par:
(C1H1) = (C1O) + (OH1) = -D + L.Cos(α1) ;
(C2H2) = (C2O) + (OH2) = -D + L.Cos(α2) ;
(O1A1) = x1 ; (O2A2) = x2
(H1A) = -L.Sin(α1) ; (H2A) = -L.Sin(α2) ;
α2 = α1 + φ
(il intervient des valeurs algébriques, de divers signes).
Il vient par conséquent:
L.Sin(α1) = (D - L.Cos(α1)(x1/d) ;
L.Sin(α2) = (D - L.Cos(α2)(x2/d) .
La détermination d'une dimension de l'objet (L) et de son orientation (α1 ou α2) exige de connaître deux distances longitudinales (d, D) en plus des abscisses (x1, x2) des points images.
Le fait de supposer l'objet relativement éloigné (L << D) simplifie les relations par approximation
L.Sin(α1) ~ D(x1/d) ,
L.Sin(α2) ~ D(x2/d) ,
mais ne supprime pas la difficulté précédente.
Rien n'empêche de faire coïncider le point (O) avec le point objet (B), ce qui revient à centrer les images sur (B1) et (B2); le problème demeure cependant, car il faut toujours résoudre le système d'équations à quatre inconnues (D, L, α1 , α2):
L.Sin(α1) = (D - L.Cos(α1)(x1/d) ;
L.Sin(α2) = (D - L.Cos(α2)(x2/d) ;
α2 = α1 + φ .
.









 Répondre avec citation
Répondre avec citation






 en bas à droite du message.
en bas à droite du message.








Partager