Bonjour,
Voici un autre raisonnement qui donne un résultat plus simple (mais pas forcément mieux, à toi d'en juger

).
Je me base sur la logique suivante:
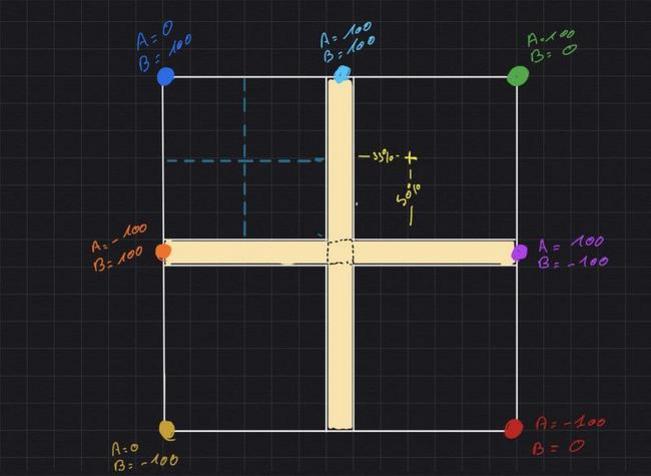
- L'axe Y représente la vitesse de déplacement du véhicule. On aimerait donc qu'il soit proportionnel à la moyenne des deux chenilles: (A + B) / 2
- L'axe X représente la vitesse de rotation du véhicule. On aimerait donc qu'il soit proportionnel à la différence des deux chenilles: A - B
En résolvant donc:
1
2
| Y = (A + B) / 2
X = (A - B) / 2 <- /2 pour simplifier le résultat |
on obtient:
Voilà, tout serait donc parfait, on respecterait les point N, E, S et O du joystick. Sauf que dans les coins, on a (A, B) = (±200, 0) ou (0, ±200). En effet, on est obligé de dépasser 100 pour "maintenir" la vitesse en tournant à la vitesse maximale.
On doit donc limiter les valeurs A et B entre -100 et 100, et on obtient donc:
1
2
| A = restriction(Y + X)
B = restriction(Y - X) |
avec
restriction qui donne 100 si c'est plus de 100 et -100 si c'est moins de -100.
Et on obtient les valeurs que tu demandes pour les 8 points extrêmes.
Mais le résultat n'est pas le même que Flodelarab dans la mesure où cela donne, pour le point donné en exemple (A, B) = (88, 17) au lieu de (66.5, 17)









 Répondre avec citation
Répondre avec citation

 en bas à droite du message.
en bas à droite du message.


Partager