1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from math import log10, log
from scipy.optimize import curve_fit
import lmfit
data=pd.read_excel('data.xlsx',sheet_name='Sheet2',index=False,dtype={'Ra': float})
print(data)
plt.xscale('log')
plt.yscale('log')
plt.scatter(np.log10(data['Ra'].values), np.log10(data['Nu_top'].values), label='Nu_top')
plt.scatter(np.log10(data['Ra'].values), np.log10(data['Nu_bottom'].values), label='Nu_bottom')
plt.errorbar(np.log10(data['Ra'].values), np.log10(data['Nu_top'].values) , yerr=data['Ecart type top'].values, linestyle="None")
plt.errorbar(np.log10(data['Ra'].values), np.log10(data['Nu_bottom'].values) , yerr=data['Ecart type bot'].values, linestyle="None")
def func(x,a):
return a*x
maxX = max(data['Ra'].values)
minX = min(data['Ra'].values)
maxY = max(data['Nu_top'].values)
minY = min(data['Nu_top'].values)
maxXY = max(maxX, maxY)
parameterBounds = [-maxXY, maxXY]
from lmfit import Model
mod = Model(func)
params = mod.make_params(a=0.25)
ret = mod.fit(np.log10(data['Nu_top'].head(10).values), params, x=np.log10(data['Ra'].head(10).values))
print(ret.fit_report())
popt, pcov = curve_fit(func, np.log10(data['Ra'].head(10).values), np.log10(data['Nu_top'].head(10).values), sigma=data['Ecart type top'].head(10).values, absolute_sigma=True, p0=[0.25])
plt.plot(np.log10(data['Ra'].head(10).values), func(np.log10(data['Ra'].head(10).values), *popt), 'r-', label='fit: a=%5.3f' % tuple(popt))
popt, pcov = curve_fit(func, np.log10(data['Ra'].tail(4).values), np.log10(data['Nu_top'].tail(4).values), sigma=data['Ecart type top'].tail(4).values, absolute_sigma=True, p0=[0.33])
plt.plot(np.log10(data['Ra'].tail(4).values), func(np.log10(data['Ra'].tail(4).values), *popt), 'b-', label='fit: a=%5.3f' % tuple(popt))
print(pcov)
plt.grid
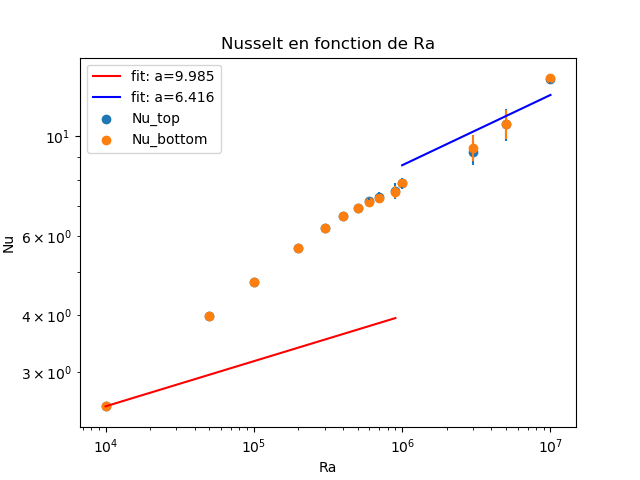
plt.title("Nusselt en fonction de Ra")
plt.xlabel('Ra')
plt.ylabel('Nu')
plt.legend()
plt.show() |









 Répondre avec citation
Répondre avec citation



Partager