Convergence trop lente

**Mani8** · 30/11/2017, 11h23

Bonjour,

Je cherche à implémenter dans Matlab un algorithme permettant de "résoudre" un réseau de tuyauterie (c'est à dire déterminer le débit Q et la direction du flux dans chaque tuyau ainsi que la hauteur piézométrique H à chaque intersection).
Le résultat obtenu est bien celui que j'attends mais pour une raison que je ne parviens pas à identifier la vitesse de convergence de l'algorithme est très lente (en témoignent les graphes de la déviation relative maximale et du résidu maximal).

Quelqu'un aurait-il un conseil pour accélérer la convergence ? Mon problème vient-il d'une fonction que j'aurais mal utilisé ?

Le code:

Code matlab :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
clear
clear all
close all
 
% Fluid and gravity
rho = 1e3;
mu  = 1e-3;
g   = 9.81;
 
% Colebrook formula
colebrook = @(Re,rr,la) 1/sqrt(la)+2*log10(rr/3.71+2.51/Re/sqrt(la));
 
% Deposit
h1 = 200;
h2 = 200;
 
% Pipe data
L1 = 600;
L2 = 400;
L3 = 900;
L4 = 400;
L6 = 350;
L7 = 600;
L9 = 300;
L10 = 500;
L11 = 300;
L12 = 350;
 
D1 = 0.5;
D2 = 0.5;
D3 = 0.5;
D4 = 0.5;
D6 = 0.5;
D7 = 0.5;
D9 = 0.3;
D10 = 0.3;
D11 = 0.3;
D12 = 0.3;
 
v_L  = [L1 L2 L3 L4 L6 L7 L9 L10 L11 L12];
v_D  = [D1 D2 D3 D4 D6 D7 D9 D10 D11 D12];
 
v_r = 1e-3*ones(1,size(v_L,2));
v_rr = v_r./v_D;
 
% Initial lambda values. Starting with Reynolds infinity.
v_la = 0.25./(log10(v_rr/3.71)).^2;
 
% Initial conditions
v_Q = 0.1*ones(1,size(v_L,2));
v_H = [10 h1 h2 10 10 10 10];
 
%Connectivity matrix
    % 1  2  3  4  6  7  8 
E = [-1  1  0  0  0  0  0; %1
     -1  0  1  0  0  0  0; %2
      1  0  0 -1  0  0  0; %3
      0  1  0 -1  0  0  0; %4
      0  0  1  0 -1  0  0; %6
      0  0  0  1 -1  0  0; %7
      0  0  1  0  0 -1  0; %9
      0  0  0  0  1 -1  0; %10
      0  0  0  0  1  0 -1; %11
      0  0  0  0  0  1 -1];%12
 
 %Declare known C values 
 x=0;
 v_C=[-0.2 x x -0.3 0 0 -0.5];
 y = [0 1 1 0 0 0 0]; %logic matrix: 0 when C is known, 1 when H is known
 
 %%....Main Loop....%%
 
 %Iteration limits
 maxiter = 1000;
 tol = 1e-3;
 inc = 1;
 res = 1;
 iter = 0;
 
 %Creation of solution storage matrices
 Q_results = zeros(size(v_Q,2),maxiter);
 H_results = zeros(size(v_H,2),maxiter);
 inc_results = zeros(1,maxiter);
 res_results = zeros(1,maxiter);
 v_sol = [v_Q v_H(1,1) v_H(1,4:size(v_H,2))];
 
 %...........MAIN LOOP.............%
 while (inc>tol) && (res>tol) && (iter<maxiter)
 
 iter = iter+1;
 
 %Storage of previous iteration results
 Q_results(:,iter)=v_Q';
 H_results(:,iter)=v_H';
 v_sol_old = v_sol;
 
 %Calculate Reynolds numbers from Q
 v_vel = 4*v_Q/pi./v_D.^2;
 v_Re  = abs(rho*v_vel.*v_D/mu);
 
 %Get the new lambdas
 for i = 1:size(v_Q,2)
    v_la(i) = fzero(@(x)colebrook(v_Re(i),v_rr(i),x),v_la(i));
 end
 
 %Obtain matrix M
 v_F = 8/pi^2/g./v_D.^4.*v_la.*v_L./v_D;
 v_K = v_F.*abs(v_Q);
 K = diag(v_K);
 M = E'/K*E;
 
 %Obtain A and b
 A=M*diag(1-y)-diag(y);
 b=-M*(v_H.*y)'+(v_C.*(1-y))';
 
 %Solve the system
 X=A\b;
 
 %Extract the new H and C values 
 v_H=X';
 v_H(2)=h1;
 v_H(3)=h2;
 v_C(2)=X(2);
 v_C(3)=X(3);
 
 %Re-evaluate Q
 v_Q=(K\E*v_H')';
 
 %Update solution matrix
 v_sol = [v_Q v_H(1,1) v_H(1,4:size(v_H,2))];
 
 %Relative increment of solution
 inc = norm((v_sol-v_sol_old)./v_sol,inf);
 %inc = norm((v_Q-v_sol_old(1:10))./v_Q,inf);
 inc_results(iter) = inc;
 
 %Residual of system
 res = norm(v_sol-v_sol_old,inf);
 %res = norm(v_Q-v_sol_old(1:10),inf);
 res_results(iter) = res;
 
 end
 
 %Plots
 inc_results(iter+1:maxiter) = [];
 res_results(iter+1:maxiter) = [];
 
 figure(1)
 subplot(211)
 semilogy(1:iter,inc_results)
 box on,grid on
 xlabel('iteration')
 ylabel('relative increment')
 
 subplot(212)
 semilogy(1:iter,res_results)
 box on,grid on
 xlabel('iteration')
 ylabel('residue')

Le système à résoudre:
Nom : Schéma réseau A.jpeg
Affichages : 750
Taille : 73,3 Ko

Détail de l'algorithme:
1- Première estimation des valeurs Q et H + estimation arbitraire de l'orientation des flux (correspond aux flèches bleues sur le schéma). Ces orientations sont consignées dans une matrice de connectivité c.a.d une matrice ayant autant de colonnes qu'il y a d'embranchements et autant de lignes qu'il y a de tuyaux. Les éléments de cette matrice valent 1 là d'où le flux part pour un tuyau donné, -1 là où il arrive et 0 partout ailleurs. Cette matrice s’appellera E.

2- Calcul de la vitesse d'écoulement v dans chaque tuyau à partir de Q=(pi*D^2/4)*v

3- Calcul du nombre de Reynolds pour chaque tuyau

4- Utilisation de la formule de Colebrook pour déterminer le coefficient de Darcy (pour la première utilisation de la formule, j'utilise une valeur du coefficient de Darcy correspondant à un nombre de Reynolds tendant vers l'infini c.a.d.
lambda=0.25/( log(eps/3.71)^2 ) )

5- Pour chaque tuyau, je calcule la valeur K=lambda/(2*g*A^2) * L/D * abs(Q) puis je crée une matrice diagonale (les K(i) formant donc une diagonale avec les autres éléments de la matrice égaux à 0)

6- On peut alors obtenir une nouvelle matrice M=E' * inv(K) * E qui présente l'avantage de vérifier l'équation suivante:
M*H=C où C désigne la somme des débits à chaque embranchement

7- Il faut alors distinguer les croisements où on connait H (II et III) et ceux où on connaît C (tous les autres).
On va construire deux nouvelles matrices. Pour chaque embranchement i :
A: - Quand C est connu, la colonne i de A est égale à la colonne i de M
- Quand H est connu, l'élément A(i,i) vaut -1 et le reste de la colonne vaut 0
b:Il s'agit un vecteur. Chaque b(i) prend initialement la valeur -1*Somme(M(i,j)*H(j)) (somme des M(i,j)*H pour tous les H connus)
- Quand C est connu, b(i)=b(i)+C
- Quand H est connu, passer à l'élément suivant
NB: J'utilise un vecteur logique (y) pour obtenir chacune de ces deux matrices avec 1 seule ligne de code

8- On peut alors résoudre A*x=b où x est un vecteur contenant pour chaque embranchement:
C si H était connu
H si C était connu

9- Je ré-obtiens alors le vecteur Q via l'équation Q=inv(K)*E*H

10- Je calcule la déviation relative par rapport à l'itération précédente ainsi que le résidu et compare à une tolérance, l'algorithme boucle alors jusqu'à ce que l'une de ces valeurs soit reconnue comme satisfaisante

**wiwaxia** · 01/12/2017, 00h54

Bonjour,

Si j'ai bien compris tes explications (sans en avoir saisi tous les détails !), tu recherches par un procédé itératif les limites des 10 composantes du vecteur débit (Q).

Que la convergence soit lente n'est pas étonnant, en raison du grand nombre des variables concernées, et de la non-linéarité des équations.

Peut-être pourrait-tu t'intéresser à la convergence séparée des diverses composantes (q₁, q₂, ... q₁₀): la stabilisation n'est-elle pas plus rapide pour certaines d'entre elles ?
Observe-t-on pour leurs valeurs successives, et à partir d'un certain stade, des suites monotones ou alternées ?

Sur le schéma apparaissent cinq termes dont dépendent tous les autres: (q₁, q₄) et d'autre part (q₂, q₅, q₇), dont la somme correspond à ce qui est fourni par les deux réservoirs:
q₁ + q₄ + q₂ + q₅ + q₇ = 0.2 + 0.3 + 0.5 = 1 m³/s .

Leurs variations ne présenteraient-elles pas, à partir d'un certain nombre d'étapes (k₀) un comportement approximativement géométrique ? Le rapport r_{j, k} = (q_{j, k+2} - q_{j, k+1}) / (q_{j, k+1} - q_{j, k})
deviendrait quasi-constant, et le remplacement toutes les deux étapes du dernier terme obtenu par une combinaison linéaire appropriée:
q'_{j, k+2} = (Ca * q_{j, k+1} + Cb * q_{j, k+2}) permettrait une accélération de la convergence.

Les valeurs: Ca = -r_j/(1 - r_j) , Cb = 1/(1 - r_j) conduisent en théorie directement à la limite;
il sera prudent de retenir pour le rapport une valeur plus modérée, donc plus proche de zéro:
# dans le cas d'une suite monotone (r_j >~ 0.9), prendre r_j = 0.5 , d'où: Ca = -1 , Cb = 2 ;
# dans le cas favorable d'une suite alternée (r_j <~ -0.9), prendre r_j = -0.5 , d'où: Ca = 1/3 , Cb = 2/3 ;
le choix encore plus simple: Ca = Cb = 0.5 (correspondant à r_j = -1) conduit souvent au résultat attendu.

**wiwaxia** · 01/12/2017, 08h58

Autre possibilité: si les cinq termes précités résultent de calculs indépendants, leur somme:
S = q₁ + q₄ + q₂ + q₅ + q₇
ne coïncide pas avec la valeur attendue S_tot = 1 m³/s .
Tu pourrais insérer après chaque itération la correction modératrice: q'_j = q_j * (S_tot/S) pour les termes concernés, avant d'en déduire tous les autres.
Mais peut-être ton algorithme en tient-il compte ?

Un procédé analogue est envisageable pour les relations de conservation du débit:
q₅ + q₆ = q₉ (noeud V),
q₇ + q₈ = q₁₀ (noeud VI),
qui consisterait à multiplier les 2 termes de la somme par le facteur f = (q_n / S_lm)^1/2, et celui de droite par son inverse f' = f^-1 .

Il faut exclure la présence de termes négatifs, au risque sinon de ralentir la convergence ou de la faire disparaître; ce qui précède ne saurait s'appliquer aux relations
q₁ + q₂ - q₃ = 0.2 , ou:
q₅ = q₉ - q₆ , par exemple.

Pour dire vrai, je doute un peu de l'efficacité de ces corrections, n'étant pas familier des équations en cause.

**Mani8** · 01/12/2017, 12h09

Merci beaucoup pour vos réponses. Je vais regarder tout ça et voir si j'arrive à accélérer un peu le processus mais il est bien possible que je doive me contenter de ce que j'ai déjà.

J'ai cependant un autre problème, le code que je vous ai donné est destiné à résoudre une version simplifiée du système (avec 3 valves fermées). Je dois donc maintenant effectuer la même opération pour le cas de figure où les valves sont ouvertes.
J'ai donc rajouté à mon code les caractéristiques des tuyaux additionnels et ai mis à jour ma matrice de connectivité (celle qui vaut 1 là où un tuyau démarre, -1 là où il finit et 0 ailleurs). Je dois aussi dans ce cas prendre en compte les pertes dues à la résistance des valves (je connais leur valeur K que je me contente donc d'ajouter à celles des tuyaux correspondant).

Cependant, dans ce cas de figure, la formule de Colebrook retourne NaN pour les deux premiers lambda à la 18ème itération.
Je reçois le message d'erreur suivant:
Exiting fzero: aborting search for an interval containing a sign change because complex function value encountered during search.
(Function value at -0.00670718 is -3.51242-13.5481i.)
Check function or try again with a different starting value.

Je ne comprends pas comment cela se fait. La formule fait intervenir la racine du précédent lambda mais j'ai vérifié et celui-ci est bien positif... Je ne vois juste pas d'où peut provenir cette valeur complexe.

EDIT: De toute évidence le problème vient des inputs de fzero, la valeur -0.0067070718 ressemble étrangement à Q(1) pour cette itération c.a.d. 6.8688*10^-4

Le système avec valves ouvertes:
Nom : Problem B.jpeg
Affichages : 662
Taille : 96,6 Ko

Nom : Problem B.jpeg
Affichages : 662
Taille : 96,6 Ko

Le code:

Code matlab :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
clear
clear all
close all
 
% Fluid and gravity
rho = 1e3;
mu  = 1e-3;
g   = 9.81;
 
% Colebrook formula
colebrook = @(Re,rr,la) 1/sqrt(la)+2*log10(rr/3.71+2.51/Re/sqrt(la));
 
% Deposit
h1 = 200;
h2 = 200;
 
% Pipe data
L1 = 600;
L2 = 400;
L3 = 900;
L4 = 400;
L6 = 350;
L7 = 600;
L9 = 300;
L10 = 500;
L11 = 300;
L12 = 350;
 
D1 = 0.5;
D2 = 0.5;
D3 = 0.5;
D4 = 0.5;
D6 = 0.5;
D7 = 0.5;
D9 = 0.3;
D10 = 0.3;
D11 = 0.3;
D12 = 0.3;
 
v_L  = [L1 L2 L3 L4 L6 L7 L9 L10 L11 L12];
v_D  = [D1 D2 D3 D4 D6 D7 D9 D10 D11 D12];
 
v_r = 1e-3*ones(1,size(v_L,2));
v_rr = v_r./v_D;
 
% Initial lambda values. Starting with Reynolds infinity.
v_la = 0.25./(log10(v_rr/3.71)).^2;
 
% Initial conditions
v_Q = 0.1*ones(1,size(v_L,2));
v_H = [10 h1 h2 10 10 10 10];
 
%Connectivity matrix
    % 1  2  3  4  6  7  8 
E = [-1  1  0  0  0  0  0; %1
     -1  0  1  0  0  0  0; %2
      1  0  0 -1  0  0  0; %3
      0  1  0 -1  0  0  0; %4
      0  0  1  0 -1  0  0; %6
      0  0  0  1 -1  0  0; %7
      0  0  1  0  0 -1  0; %9
      0  0  0  0  1 -1  0; %10
      0  0  0  0  1  0 -1; %11
      0  0  0  0  0  1 -1];%12
 
 %Declare known C values 
 Unknown=0;
 v_C=[-0.2 Unknown Unknown -0.3 0 0 -0.5];
 y = [0 1 1 0 0 0 0]; %logic matrix: 0 when C is known, 1 when H is known
 
 %%....Main Loop....%%
 
 %Iteration limits
 maxiter = 1000;
 tol = 1e-9;
 inc = 1;
 res = 1;
 iter = 0;
 
 %Creation of solution storage matrices
 Q_results = zeros(size(v_Q,2),maxiter);
 H_results = zeros(size(v_H,2),maxiter);
 inc_results = zeros(1,maxiter);
 res_results = zeros(1,maxiter);
 v_sol = [v_Q v_H(1,1) v_H(1,4:size(v_H,2))];
 
 X=zeros(size(v_H,2),1);
 
 %...........MAIN LOOP.............%
 while (inc>tol) && (res>tol) && (iter<maxiter)
 
 iter = iter+1;
 
 %Storage of previous iteration results
 Q_results(:,iter)=v_Q';
 H_results(:,iter)=v_H';
 v_sol_old = v_sol;
 
 X_old=X;
 
 %Calculate Reynolds numbers from Q
 v_vel = 4*v_Q/pi./v_D.^2;
 v_Re  = abs(rho*v_vel.*v_D/mu);
 
 %Get the new lambdas
 for i = 1:size(v_Q,2)
    v_la(i) = fzero(@(x)colebrook(v_Re(i),v_rr(i),x),v_la(i));
 end
 
 %Obtain matrix M
 v_F = 8/pi^2/g./v_D.^4.*v_la.*v_L./v_D;
 v_K = v_F.*abs(v_Q);
 K = diag(v_K);
 M = E'/K*E;
 
 %Obtain A and b
 A=M*diag(1-y)-diag(y);
 b=-M*(v_H.*y)'+(v_C.*(1-y))';
 
 %Solve the system
 X=A\b;
 
 %Extract the new H and C values 
 v_H=X';
 v_H(2)=h1;
 v_H(3)=h2;
 v_C(2)=X(2);
 v_C(3)=X(3);
 
 %Re-evaluate Q
 v_Q=(K\E*v_H')';
 
 %Update solution matrix
 v_sol = [v_Q v_H(1,1) v_H(1,4:size(v_H,2))];
 
 %Relative increment of solution
 %inc = norm((v_sol-v_sol_old)./v_sol,inf);
 %inc = norm((v_Q-v_sol_old(1:10))./v_Q,inf);
 inc = norm((X-X_old)./X,inf);
 inc_results(iter) = inc;
 
 %Residual of system
 %res = norm(v_sol-v_sol_old,inf);
 res = norm(v_Q-v_sol_old(1:10),inf);
 res_results(iter) = res;
 
 end
 
 %Plots
 inc_results(iter+1:maxiter) = [];
 res_results(iter+1:maxiter) = [];
 
 figure(1)
 subplot(211)
 semilogy(1:iter,inc_results)
 box on,grid on
 xlabel('iteration')
 ylabel('relative increment')
 
 subplot(212)
 semilogy(1:iter,res_results)
 box on,grid on
 xlabel('iteration')
 ylabel('residue')

**wiwaxia** · 01/12/2017, 13h19

Il faut s'attendre à ce que le 3^me réservoir, situé nettement plus haut, bouleverse la répartition des flux à l'ouverture des vannes, et inverse le sens de circulation du fluide dans quelques unes des conduites.

Est-il possible de suivre en parallèle les valeurs successives des 14 composantes du vecteur (Q) ? Cela te permettrait de repérer où se produit la première inversion de signe ...
La notation indiquée dans le second schéma est choquante: tu as sans doute de bonnes raisons de l'avoir adoptée, mais j'aurais pour ma part réservé les quatre derniers indices (11, 12 ... 14) aux conduites munies d'une vanne, et dont on peut commander la mise en service.

Et à la réflexion, ce changement de notation est inéluctable, si tu veux maîtriser algorithmiquement l'évolution du réseau d'un état à l'autre (vannes toutes ouvertes ou fermées), avec à la clef l'éventualité de n'en ouvrir que quelques unes ...

: les conduites présentes doivent impérativement recevoir les mêmes indices.

Les inversions de signe deviennent à priori gérables au prix d'un petit changement, dans l'expression de la formule de Darcy:

Nom : Formule de Darcy.png
Affichages : 1096
Taille : 190,7 Ko

Nom : Formule de Darcy.png
Affichages : 1096
Taille : 190,7 Ko

, en remplaçant V² par le produit V*Abs(V) .

PS: le plantage de ton programme provient de la formule de Colebrook, au niveau du nombre de Reynolds: il faut là encore y remplacer (V) par Abs(V).

**Mani8** · 01/12/2017, 15h19

Merci beaucoup pour votre aide !!!
J'ai utilisé cette notation pour la simple raison que c'est celle employée dans mon énoncé mais votre remarque est très sensée. Je pense que je vais procéder comme vous le dites, quitte à remettre les résultats dans l'ordre en post-process.

**tbc92** · 01/12/2017, 16h04

Une question :
On a un premier schéma, qui correspond à la situation 'Valves fermées'.
Puis un autre schéma, pour la situation 'Valves ouvertes'.
La question, c'est
Réponse 1 : Etudier indépendamment, le schéma 1, et le schéma 2
Réponse 2 : Etudier ce qui se passe un peu après l'ouverture de telle ou telle vanne.

Ma participation va probablement se limiter à ça : éviter les quiproquos.

**Mani8** · 01/12/2017, 17h37

On me demande d'étudier deux cas de figure différents dans lesquels:
1) Toutes les valves sont fermées et le système est stable
2) Toutes les valves sont ouvertes, le système est là aussi considéré dans son état stable

**Mani8** · 01/12/2017, 18h46

Bon ça faisait quelques heures que je m'acharnait sur le cas B sans parvenir à résoudre le problème alors j'ai demandé à un ami de me montrer son code fonctionnel qui est le suivant:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
%1.Define data 
%1.0.Simple data
rho=1000;
g=9.8;
mu=0.001;
eps=0.001;
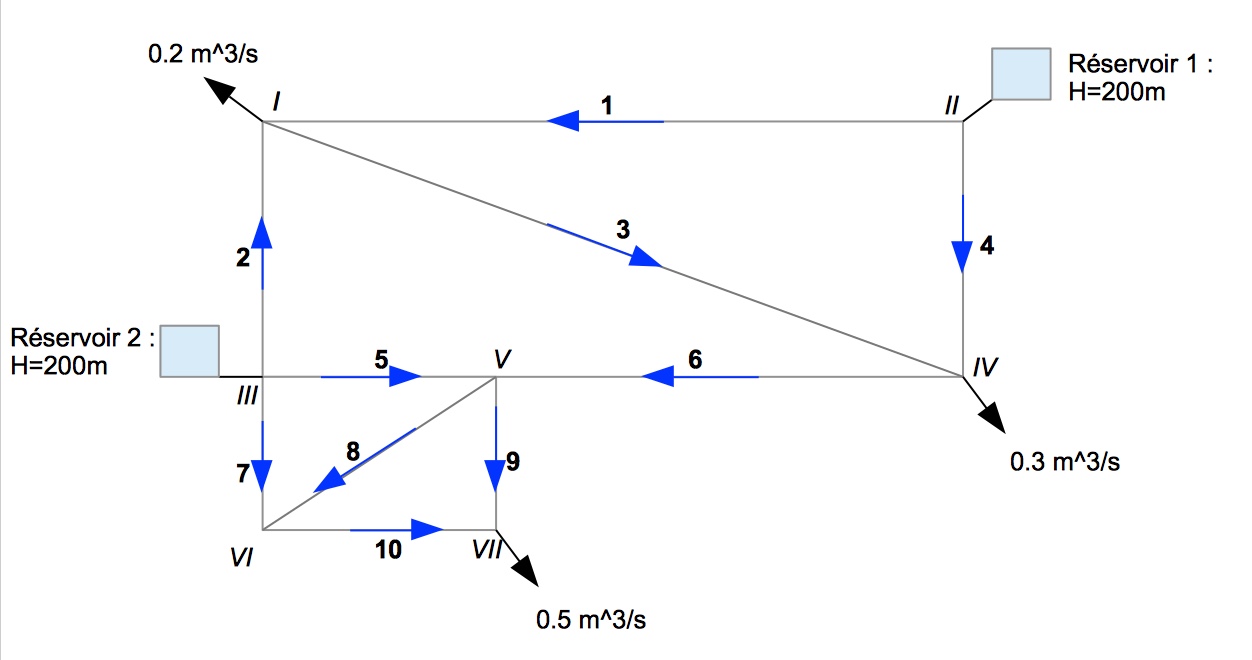
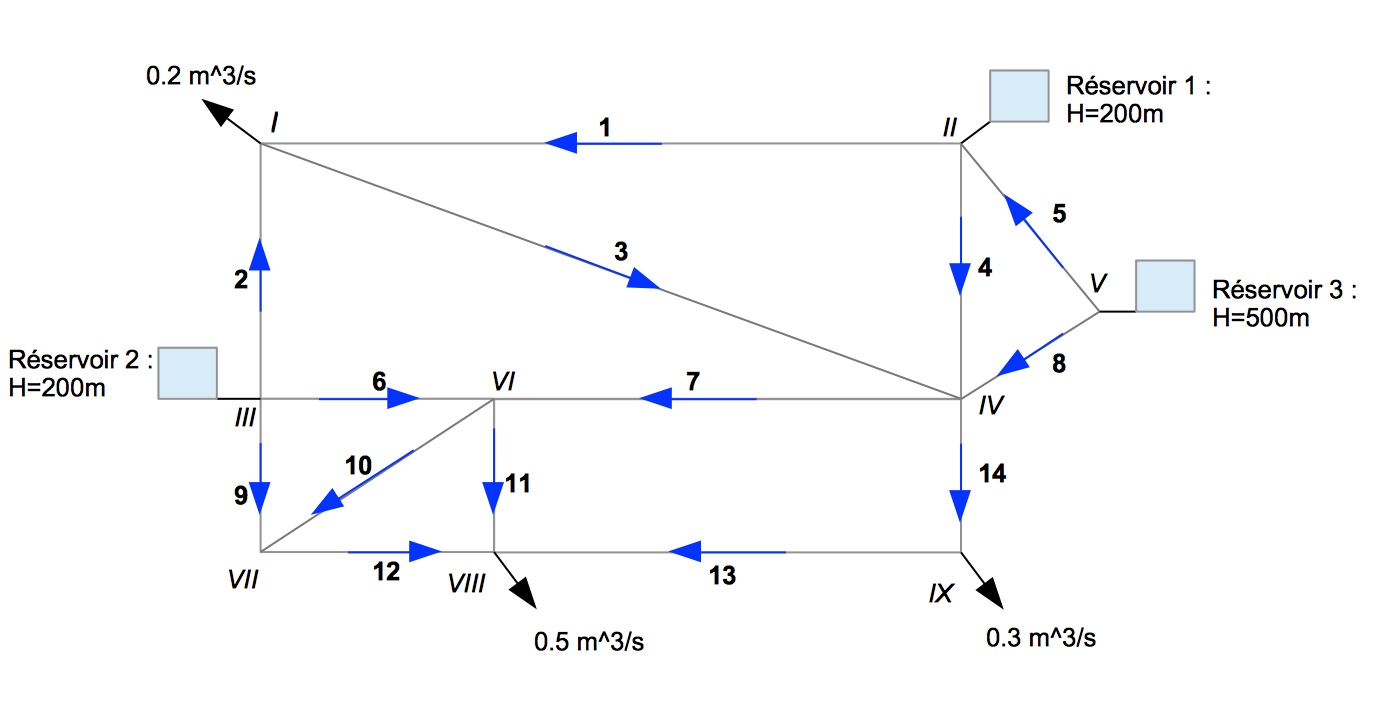
NN=9;
NE=14;
error=0.0001;
%1.1.Conectivity matrix
E= [1 -1 0 0 0 0 0 0 0;
    1 0 -1 0 0 0 0 0 0;
    1 0 0 -1 0 0 0 0 0;
    0 1 0 -1 0 0 0 0 0;
    0 1 0 0 -1 0 0 0 0;
    0 0 1 0 0 -1 0 0 0;
    0 0 0 1 0 -1 0 0 0;
    0 0 0 1 -1 0 0 0 0;
    0 0 1 0 0 0 -1 0 0;
    0 0 0 0 0 1 -1 0 0;
    0 0 0 0 0 1 0 -1 0;
    0 0 0 0 0 0 1 -1 0;
    0 0 0 0 0 0 0 1 -1;
    0 0 0 1 0 0 0 0 -1];
%1.2.Lengths vector
L=[600;400;900;400;400;350;600;400;300;500;300;350;600;300];
%1.3.Diameters vector
D=[0.5;0.5;0.5;0.5;0.4;0.5;0.5;0.4;0.3;0.3;0.3;0.3;0.3;0.3];
%1.4.Inflows at the nodes vector. The unknown inflows will be set to zero
%initially, and then will change its value (C2, C3, C5)
C=[-0.2;0;0;0;0;0;0;-0.5;-0.3];
%1.5.Piezometric heights vector. 
H=[0;200;200;0;500;0;0;0;0];
%1.6.Boolean vector that determines whether we know the inflow Ci or the
%piezometric height Hi (1 for known C and 0 for known H)
BOOL=[1;0;0;1;0;1;1;1;1];
%1.7.Valves f vector
F=[0;0;0;0;10;0;0;15;0;0;0;0;10;0];
%1.8.Initialise Q vector
Q=ones(NE,1);
%1.9.Initialise Lambdas vector
LA=zeros(NE,1);
for i=1:NE
    LA(i)=(-2*log(eps/(D(i)*3.7))/log(10))^-2;
end
 
%2.Problem solution
BOOL2=1;
iteration=1;
RELQ=zeros(NE,100000);
RELX=zeros(NE,100000);
MEMX=zeros(NN,100000);
MEMQ=[Q,zeros(NE,100000-1)];
RESIDUALS=zeros(NE,100000);
 
while BOOL2==1
    %2.1.Define K matrix (diagonal, such that E*H=K*Q)
    K=diag([zeros(1,NE)]);
    for i=1:NE
        K(i,i)=8*abs(Q(i))*(LA(i)*L(i)/D(i)+F(i))/(g*pi^2*D(i)^4);
    end
 
    %Calculate residuals for the problem (from the previous iteration
    RESIDUALS(:,iteration)=abs(Q-((K\E)*H));
 
    %2.2.Define M matrix as tras(E)*inv(K)*E
    M=E'*(K\E);      
    %2.3.Use of the algorithm (shown in class) to find the A matrix.
    A=zeros(NN,NN);
    for j=1:NN
        %Known C(j)
        if BOOL(j)==1
            for i=1:NN
                A(i,j)=M(i,j);
            end
        %Known H(j)
        else
            for i=1:NN
                if i==j
                    A(i,j)=-1;
                end
            end
        end
    end
    %2.4.Use of the algorithm to find b vector
    b=zeros(NN,1);
    for i=1:NN
        for j=1:NN
            b(i)=b(i)-M(i,j)*(H(j)*(1-BOOL(j)));
        end
        if BOOL(i)==1
            b(i)=b(i)+C(i);
        end
    end
    %Solve the system of equations A*x=b
    x=A\b;
    %Set the values of x into the correspondent vector (either H or C)
    for i=1:NN
        if BOOL(i)==1
            H(i)=x(i);
        else
            C(i)=x(i);
        end
    end
    %Compute Q
    Q=K\E*H;
    %Store values of Q and X in two matrices
    for i=1:NE
        MEMQ(i,iteration+1)=Q(i);
    end
    for i=1:NN
        MEMX(i,iteration+1)=x(i);
    end
    %Calculate relative increments for Q and X
    for i=1:NE
        RELQ(i,iteration)=abs((MEMQ(i,iteration+1)-MEMQ(i,iteration))/MEMQ(i,iteration+1));
    end
    for i=1:NN
        RELX(i,iteration)=abs((MEMX(i,iteration+1)-MEMX(i,iteration))/MEMX(i,iteration+1));
    end
 
    %Compare relative increments and residuals with the error limit
    BOOL2=0;
 
        if max(RELQ(:,iteration))>=error
            BOOL2=1;
        end
        if max(RELX(:,iteration))>=error
            BOOL2=1;
        end
        if max(RESIDUALS(:,iteration))>=error
            BOOL2=1;
        end
        %Recalculate lambda before next iteration
        RE=zeros(NE,1);
    for i=1:NE
        RE(i)=4*rho*abs(Q(i))/(pi*mu*D(i));
    end
    for j=1:10
        for i=1:NE
            LA(i)=(-2*log((eps/(D(i)*3.7))+(2.51/(RE(i)*sqrt(LA(i)))))/log(10))^-2;
        end
    end
    iteration=iteration+1;
    if (iteration==100000)
        BOOL2=0;
    end
end  
PLOT1=zeros(iteration,1);
PLOT2=zeros(iteration,1);
PLOT3=zeros(iteration,1);
for i=1:iteration
    PLOT1(i)=max(RELQ(:,i));
    PLOT2(i)=max(RELX(:,i));
    PLOT3(i)=max(RESIDUALS(:,i));  
end
semilogy(PLOT1)
semilogy(PLOT2)
semilogy(PLOT3)

Comme il n'est pas dans ma nature de copier bêtement sans comprendre ce que je fais, j'ai tenté de lire son code pour y identifier les divergences avec le mien pour réparer ce dernier.
Je me suis aperçu que, plutôt que d'utiliser fzero pour estimer Lambda via la formule de Colebrook, sa méthode consiste plutôt à calculer directement sa valeur en définissant le lambda du membre de gauche comme la valeur au rang k+1 tandis que le lambda du membre de droite est celui de l'itération précédente.
lambda(k+1) = ( -2*log10( RR/3.71 + 2.51/( abs(Re)*sqrt(lambda(k)) )^-2
Ça m'a parut étrange mais j'ai quand même essayé d'utiliser cette méthode dans mon propre code:

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
clear
clear all
close all
 
% Fluid and gravity
rho = 1e3;
mu  = 1e-3;
g   = 9.81;
 
% Colebrook formula
colebrook = @(Re,rr,la) 1/sqrt(la)+2*log10(rr/3.71+2.51/abs(Re)/sqrt(la));
 
% Deposit
h1 = 200;
h2 = 200;
h3 = 500;
 
% Pipe data
L1 = 600;
L2 = 400;
L3 = 900;
L4 = 400;
L5 = 400;
L6 = 350;
L7 = 600;
L8 = 400;
L9 = 300;
L10 = 500;
L11 = 300;
L12 = 350;
L13 = 600;
L14 = 300;
 
D1 = 0.5;
D2 = 0.5;
D3 = 0.5;
D4 = 0.5;
D5 = 0.4;
D6 = 0.5;
D7 = 0.5;
D8 = 0.4;
D9 = 0.3;
D10 = 0.3;
D11 = 0.3;
D12 = 0.3;
D13 = 0.3;
D14 = 0.3;
v_L  = [L1 L2 L3 L4 L5 L6 L7 L8 L9 L10 L11 L12 L13 L14];
v_D  = [D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14];
 
v_r = 1e-3*ones(1,size(v_L,2));
v_rr = v_r./v_D;
 
% Initial lambda values. Starting with Reynolds infinity.
v_la = 0.25./(log10(v_rr/3.71)).^2;
 
% Initial conditions
v_Q = 0.1*ones(1,size(v_L,2));
v_H = [10 h1 h2 10 h3 10 10 10 10];
 
%Connectivity matrix
    % 1  2  3  4  5  6  7  8  9
E = [-1  1  0  0  0  0  0  0  0; %1
     -1  0  1  0  0  0  0  0  0; %2
      1  0  0 -1  0  0  0  0  0; %3
      0  1  0 -1  0  0  0  0  0; %4
      0 -1  0  0  1  0  0  0  0; %5
      0  0  1  0  0 -1  0  0  0; %6
      0  0  0  1  0 -1  0  0  0; %7
      0  0  0 -1  1  0  0  0  0; %8
      0  0  1  0  0  0 -1  0  0; %9
      0  0  0  0  0  1 -1  0  0; %10
      0  0  0  0  0  1  0 -1  0; %11
      0  0  0  0  0  0  1 -1  0; %12
      0  0  0  0  0  0  0 -1  1; %13
      0  0  0  1  0  0  0  0 -1;];%14
 
 
 %Declare known C values 
 Unknown=0;
 v_C=[-0.2 Unknown Unknown 0 Unknown 0 0 -0.5 -0.3];
 y = [0 1 1 0 1 0 0 0 0]; %logic matrix: 0 when C is known, 1 when H is known
 
 %%....Main Loop....%%
 
 %Iteration limits
 maxiter = 1000;
 tol = 1e-3;
 inc = 1;
 res = 1;
 iter = 0;
 
 %Creation of solution storage matrices
 Q_results = zeros(size(v_Q,2),maxiter);
 H_results = zeros(size(v_H,2),maxiter);
 inc_results = zeros(1,maxiter);
 res_results = zeros(1,maxiter);
 v_sol = [v_Q v_H(1) v_H(4) v_H(1,6:size(v_H,2))];
 
 %...........MAIN LOOP.............%
 while (inc>tol) && (res>tol) && (iter<maxiter)
 
 iter = iter+1;
 
 %Storage of previous iteration results
 Q_results(:,iter)=v_Q';
 H_results(:,iter)=v_H';
 v_sol_old = v_sol;
 
 %Calculate Reynolds numbers from Q
 v_vel = 4*abs(v_Q)/pi./v_D.^2;
 v_Re  = abs(rho*abs(v_vel).*v_D/mu);
 
 %Get the new lambdas
 %for i = 1:size(v_Q,2)
 %   v_la(i) = fzero(@(x)colebrook(v_Re(i),v_rr(i),x),v_la(i));
 %end
 
 v_la=(-2*log10(v_rr/3.71+2.51./(abs(v_Re).*sqrt(v_la)))).^2;
 
 %Obtain matrix M
 v_F = 8/pi^2/g./v_D.^4.*v_la.*v_L./v_D;
 v_K = v_F.*abs(v_Q);
 v_K(5) = v_K(5)+10; %Add pumps' K values
 v_K(8) = v_K(8)+15;
 v_K(13) = v_K(13)+10;
 K = diag(v_K);
 M = E'/K*E;
 
 %Obtain A and b
 A=M*diag(1-y)-diag(y);
 b=-M*(v_H.*y)'+(v_C.*(1-y))';
 
 %Solve the system
 X=A\b;
 
 %Extract the new H and C values 
 v_H=X';
 v_H(2)=h1;
 v_H(3)=h2;
 v_H(5)=h3;
 v_C(2)=X(2);
 v_C(3)=X(3);
 v_C(5)=X(5);
 
 %Re-evaluate Q
 v_Q=(K\E*v_H')';
 
 %Update solution matrix
 v_sol = [v_Q v_H(1) v_H(4) v_H(1,6:size(v_H,2))];
 
 %Relative increment of solution
 inc = norm((v_sol-v_sol_old)./v_sol,inf);
 %inc = norm((v_Q-v_sol_old(1:10))./v_Q,inf);
 inc_results(iter) = inc;
 
 %Residual of system
 res = norm(v_sol-v_sol_old,inf);
 %res = norm(v_Q-v_sol_old(1:10),inf);
 res_results(iter) = res;
 
 end
 
 %Plots
 inc_results(iter+1:maxiter) = [];
 res_results(iter+1:maxiter) = [];
 
 figure(1)
 subplot(211)
 semilogy(1:iter,inc_results)
 box on,grid on
 xlabel('iteration')
 ylabel('relative increment')
 
 subplot(212)
 semilogy(1:iter,res_results)
 box on,grid on
 xlabel('iteration')
 ylabel('residue')

Résultat le code ne plante plus mais l'algorithme de converge tout simplement pas...
Le problème viendrait-il d'ailleurs ?

**wiwaxia** · 02/12/2017, 09h13

Envoyé par Mani8

... Comme il n'est pas dans ma nature de copier bêtement sans comprendre ce que je fais, j'ai tenté de lire son code pour y identifier les divergences avec le mien pour réparer ce dernier.
Je me suis aperçu que, plutôt que d'utiliser fzero pour estimer Lambda via la formule de Colebrook, sa méthode consiste plutôt à calculer directement sa valeur en définissant le lambda du membre de gauche comme la valeur au rang k+1 tandis que le lambda du membre de droite est celui de l'itération précédente.
lambda(k+1) = ( -2*log10( RR/3.71 + 2.51/( abs(Re)*sqrt(lambda(k)) )^-2
Ça m'a parut étrange mais j'ai quand même essayé d'utiliser cette méthode dans mon propre code: ...

... Résultat le code ne plante plus mais l'algorithme de converge tout simplement pas ...
Le problème viendrait-il d'ailleurs ?

Coupler la suite itérative Lambda_k+1 = F(Lambda_k+1) à celle censée conduire aux solutions limites (q₁, q₂, ...) ne conduit à rien, parce que c'est confondre le procédé itératif permettant de connaître la racine (Lambda) de l'équation de Colebrook (pour des valeurs données des deux autres paramètres RR, Re) avec celui qui donne accès à la répartition des flux, par approximations successives.

Nom : Formule de Colebrook.png
Affichages : 959
Taille : 61,3 Ko

Nom : Formule de Colebrook.png
Affichages : 959
Taille : 61,3 Ko

Il faut à chaque étape disposer de la valeur exacte de Lambda pour établir le lien entre débit et perte de charge au niveau de chaque conduite, ce qu'effectue (si je ne trompe pas) l'instruction

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

v_la(i) = fzero(@(x)colebrook(v_Re(i),v_rr(i),x),v_la(i));

appelant une recherche de zéro sur la fonction

Code :

Sélectionner tout - Visualiser dans une fenêtre à part

colebrook = @(Re,rr,la) 1/sqrt(la)+2*log10(rr/3.71+2.51/Re/sqrt(la));

Je n'ai pas testé la résolution de cette équation, faute de disposer des valeurs des autres paramètres (RR, Re).

Convergence trop lente

Algorithmes et structures de données

Discussions similaires

Partager

Partager