Bonsoir,
@tbc92
La généralisation de la définition de l'ellipse à un nombre quelconque de points est en soi intéressante
cependant je ne crois pas que les courbes obtenues soient des quadriques; en effet, si l'élimination des radicaux ne pose aucun problème dans le cas du cercle et de l'ellipse, par une ou deux élévations au carré :
L = d1 _____________________________ L2 = d12
L = d1 + d2 _________________________ (L2 - d12 - d22)2 = 4 * (d12) * (d22)
il n'en va plus de même à partir de trois termes, parce qu'il n'est plus possible de réduire le nombre de radicaux présents; il suffit de regarder ce que donne un traitement analogue de la relation : L = d1 + d2 + d3 ).
Il ne s'agit plus alors de courbes algébriques.
Un document contenant d'assez belles représentations de ces courbes peut être téléchargé depuis ce site.
Elles sont toujours convexes, à moins qu'il intervienne des coefficients de signes opposés (par une extension moins intuitive de la définition de l'hyperbole:
L = │d1 - d2│ .
https://fr.wikipedia.org/wiki/Point_de_Fermat
http://www.mathcurve.com/surfaces/quadric/quadric.shtml











 Répondre avec citation
Répondre avec citation











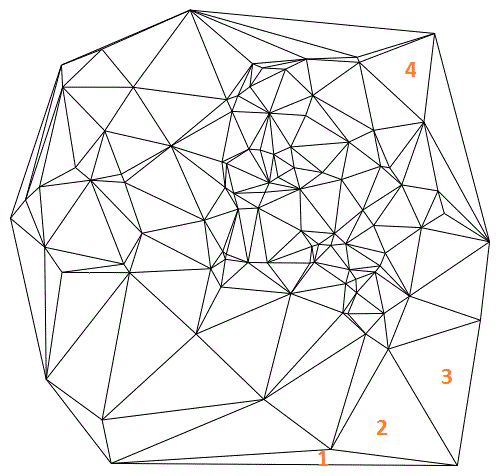
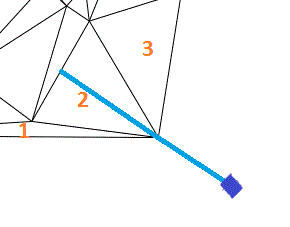
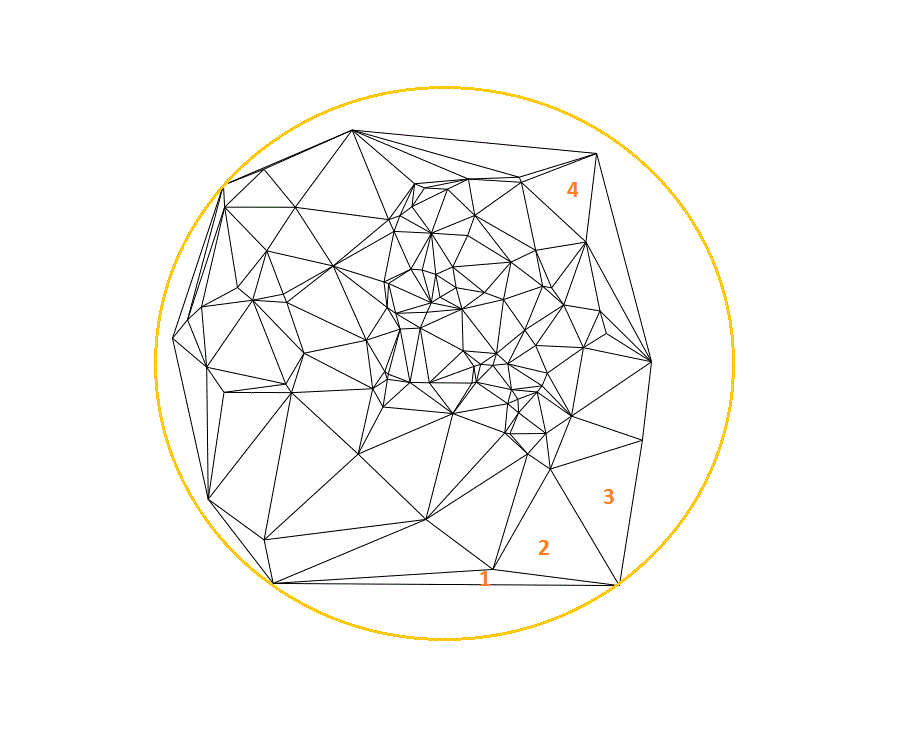
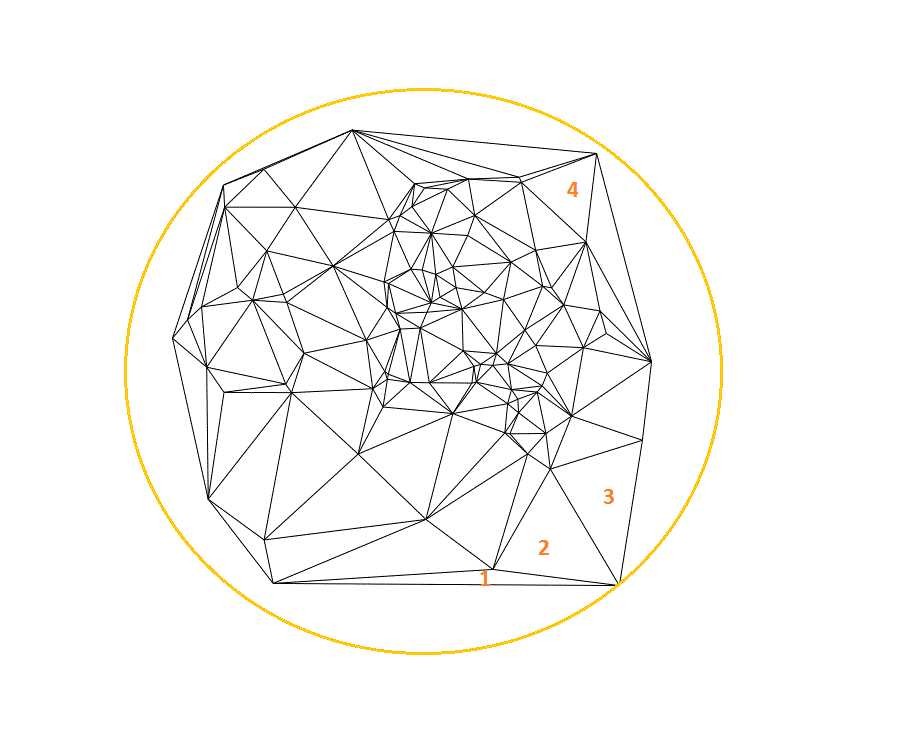
 : Sinon l'échange dérive vers
: Sinon l'échange dérive vers ![Nom : Doc [2016-06-04] Cercle Delaunay_03.jpg
Affichages : 493
Taille : 59,5 Ko](https://www.developpez.net/forums/attachments/p211861d1465138242/general-developpement/algorithme-mathematiques/mathematiques/contraire-d-barycentre/doc-2016-06-04-cercle-delaunay_03.jpg/)

Partager